Desde los tiempos de Newton, los matemáticos buscaban herramientas para explicar fenómenos dinámicos: movimiento, crecimiento o variaciones en el tiempo. Así nacieron los conceptos de límite y derivada, que hoy son pilares en la enseñanza del cálculo.
Así que, si llegaste hasta aquí ¡estás a punto de hallar tus respuestas! Sea que busques un refuerzo matemático o quieras dominar estos componentes matemáticos clave, en Superprof Chile hemos preparado esta guía introductoria completa para estudiantes como tú, con interés de aprender y dominar estos dos conceptos básicos del cálculo: Además, puedes acceder a clases de matemáticas para reforzar lo aprendido.

Introducción a los límites y derivadas
Cuando escuchamos hablar de cálculo, inmediatamente pensamos en conceptos como límite y derivada. Estos son la base del análisis matemático moderno y permiten comprender fenómenos en física, economía, tecnología y muchas otras áreas.
Pero, tranquilo, que iremos paso a paso para que puedas conocer: la definición de límites y derivaciones, ejemplos prácticos, aplicaciones y recursos útiles para que cualquier estudiante pueda aprenderlos con confianza.
¿Por qué son importantes en el estudio del cálculo?
El límite y la derivada son herramientas fundamentales para describir cómo cambian las funciones. Gracias a ellos, podemos analizar la continuidad, calcular la pendiente de una recta tangente y resolver problemas que parecen imposibles con simples operaciones algebraicas.
Diferencias y conexiones entre límite y derivada
Límite
- Analiza el comportamiento de una función al aproximarse a un valor.
- Puede existir aunque la función no esté definida en ese punto.
- Es un concepto del cálculo más general.
Derivada
- Mide la rapidez de cambio de una función en un punto específico.
- Es un valor que requiere continuidad y ser diferenciable.
- Su existencia es particularmente definida usando los límites.
Aplicaciones prácticas en ciencia, economía y física
¡El cálculo no queda solo en tu cuaderno de la escuela! Y es que sí, entender los límites y las derivadas no es solo un ejercicio académico. Estas herramientas son parte del análisis matemático fundamental, porque permiten resolver problemas que involucran funciones, variables en constante cambio y situaciones donde intervienen conceptos como la continuidad, el infinito o la pendiente de una curva. Gracias al cálculo, podemos conectar la teoría con la vida real y dar soluciones prácticas en diferentes disciplinas, lo podremos ver en:
🌌Física
Los físicos usan derivadas para calcular la velocidad instantánea (cambio de posición respecto al tiempo) y la aceleración (cambio de velocidad).
El límite permite definir magnitudes cuando una variable se aproxima a un valor cero o al infinito, por ejemplo en el estudio de ondas o trayectorias orbitales. Mientras que, la integral se aplica para obtener áreas bajo curvas que representan trabajo, energía o flujo de partículas.
📈 Economía
Con el cálculo diferencial, se encuentran mínimos y máximos de funciones de costos, ingresos y beneficios, lo que ayuda en procesos de optimización.
Se utilizan las derivadas para analizar tasas de variación en precios, producción o demanda, permitiendo proyectar tendencias del mercado. ¿Ya lo ves? En este campo, el cálculo integral sirve para estimar acumulados como ingresos totales o consumo en intervalos de tiempo.
💻 Tecnología
En informática y gráficos por computadora, la derivación se usa para trazar la recta tangente en curvas y suavizar animaciones en 3D.
Las integrales ayudan en el procesamiento digital de señales, en algoritmos de compresión y en cálculos de áreas y volúmenes. Al integrar el análisis con funciones continuas y diferenciables en el mundo tecnológico, es posible desarrollar los ya afamados modelos predictivos que se implementan en software de simulación e incluso, tienen parte en el desarrollo de nuevas tecnologías IA.
🧪 Otras aplicaciones
- En biología, se aplican para modelar el crecimiento poblacional con funciones exponenciales y analizar tasas de cambio de especies.
- En química, ayudan a describir reacciones donde las concentraciones dependen de varias variables.
- En ingeniería, se emplea la regla del producto o el cociente para resolver ecuaciones diferenciales que modelan estructuras, fluidos o circuitos eléctricos.
¿Qué es un límite? Definición y explicación
Un límite nos dice qué valor “se aproxima” a tomar una función cuando la variable se acerca a un número en particular. No significa necesariamente que la función tenga un valor exacto en ese punto, sino que observamos hacia dónde tiende su comportamiento.
Por ejemplo, si escribimos:
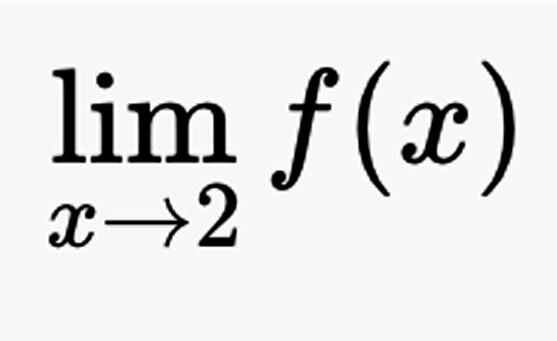
Lo que queremos expresar es: “cuando x se acerca al número 2, ¿hacia qué valor se acerca la función f(x)?”. Es como seguir con la mirada una curva en la gráfica y ver qué número está “esperando” cuando nos acercamos al 2 desde la izquierda o desde la derecha.
Representación gráfica y conceptual
En una gráfica, un límite puede observarse siguiendo la curva a medida que nos acercamos a cierto valor de la variable. Incluso cuando la función no está definida en ese punto, el límite puede existir. Esto es clave para entender la continuidad y las funciones diferenciables.
¿Conoces las propiedades matemáticas de un límite?
Ejemplo práctico para entender un límite
En una gráfica, un límite puede observarse siguiendo la curva a medida que nos acercamos a cierto valor de la variable. Incluso cuando la función no está definida en ese punto, el límite puede existir. Esto es clave para entender la continuidad y las funciones diferenciables.
Veámoslo:
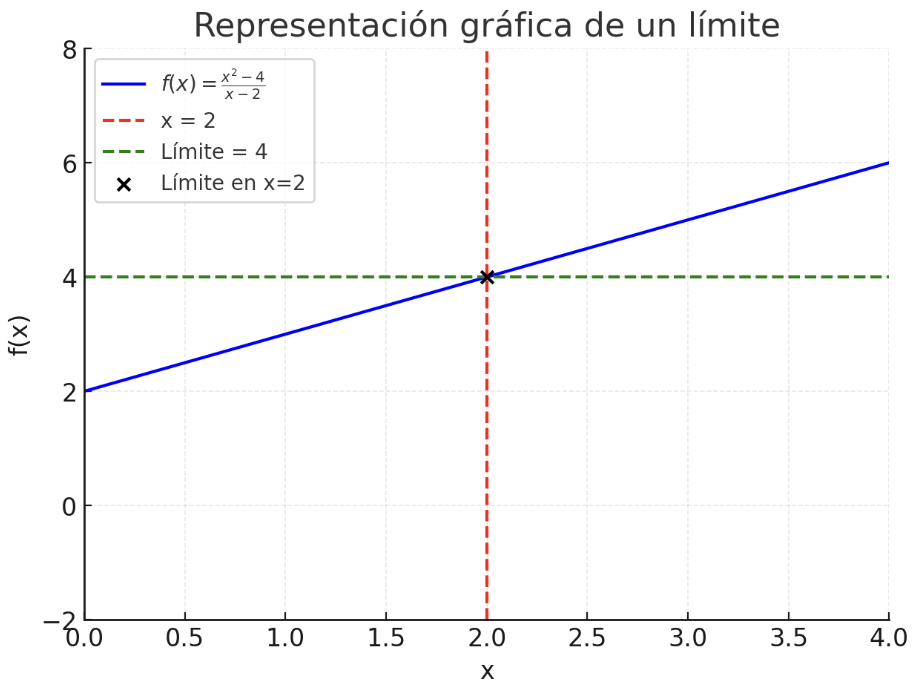
La función :
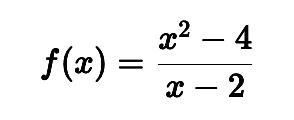
¿Lo ves? no está definida en 𝑥=2 (porque genera una división por cero). Sin embargo, al observar la gráfica, verás que cuando 𝑥 se acerca a 2, la función se acerca al valor 4.
Esto demuestra que el límite existe aunque la función no tenga un valor definido en ese punto. Descubre más de este concepto aquí.
¿Qué es una derivada? Definición y relación con los límites
La derivada es una herramienta fundamental del cálculo, ya que nos permite analizar cómo varía una función cuando su variable independiente cambia. Dicho de forma sencilla: mide la tasa de cambio instantánea. Por ejemplo, en física, si la función describe la posición de un objeto, su derivada nos da la velocidad en un punto específico.
En términos matemáticos, la derivada se obtiene a partir de un límite. Se define como el límite del cociente incremental:
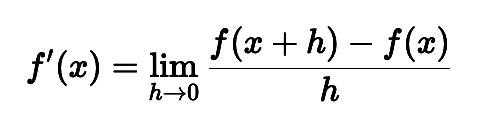
Aquí:
- El numerador representa la diferencia entre dos valores de la función.
- El cociente expresa la pendiente de la recta secante que une esos dos puntos.
- Al aplicar el límite cuando ℎ→0, esa secante se convierte en la recta tangente, lo que nos da la pendiente exacta en un punto.
¿Cómo se relaciona con el concepto de pendiente?
La derivada en un punto nos indica la pendiente de la recta tangente a la gráfica de la función.
Esto significa conocer la inclinación exacta de la curva en un instante, no solo un promedio.
En otras palabras, la derivada traduce el cambio de la función en una medida precisa de variación instantánea.
¿Qué tanto sabes de las derivaciones matemáticas?
Ejemplo simple con función lineal o cuadrática
Si tomamos la función:
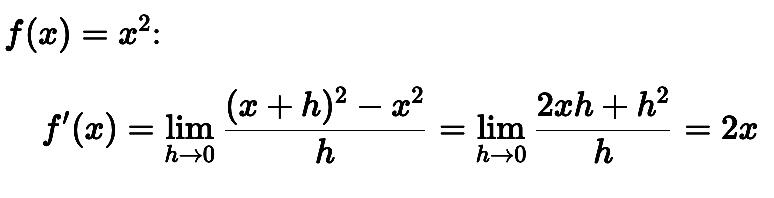
Esto significa que la pendiente en cada punto es el doble de su valor en x.

Ejercicios básicos de límites y derivadas
Antes de dominar el cálculo, es fundamental practicar con ejemplos sencillos. Los ejercicios de límites y derivadas permiten afianzar la teoría, visualizar cómo cambian las funciones y aprender a resolver problemas paso a paso con mayor seguridad. Así que, concéntrate en los siguientes ejemplos: Si necesitas apoyo personalizado, en Superprof puedes encontrar clases particulares de matemática.
Ejercicio resuelto paso a paso: cálculo de un límite
Calcular:
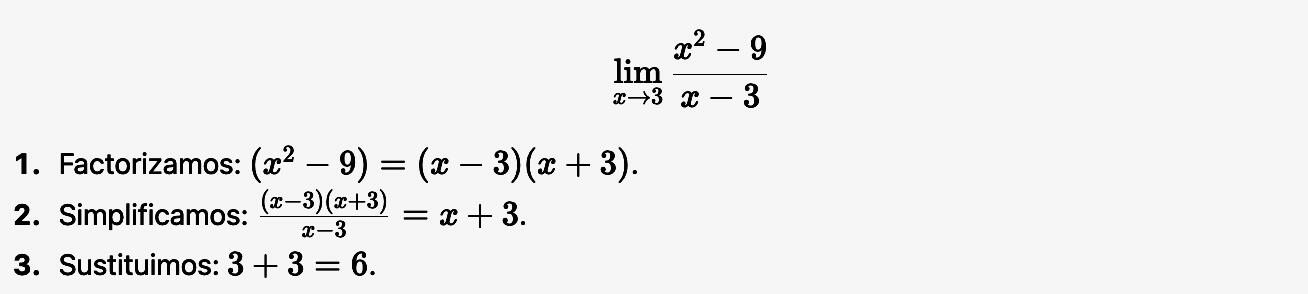
Resultado: el límite es 6.
Ejercicio resuelto paso a paso: cálculo de una derivada
Calcular:
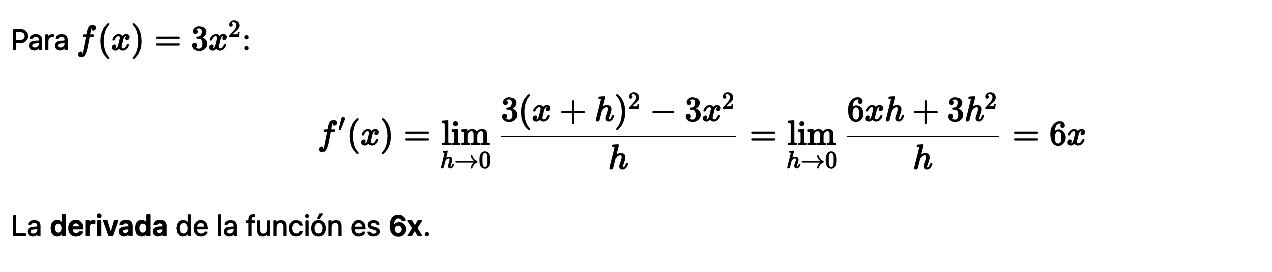
Casos comunes de errores y cómo evitarlos
- Confundir el valor de la función con el límite.
- Olvidar que el denominador no puede ser cero al sustituir.
- Aplicar mal la regla de la derivación (por ejemplo, producto o cociente).
En esta sección también recomendamos practicar con ejercicios de límites y derivadas, ya que resuelven dudas frecuentes y consolidan el aprendizaje.
Aprende cuáles son las reglas básicas de una derivación ¡aquí!
¿Para qué sirven los límites y derivadas en la vida real?
Los límites y derivadas no son solo teoría abstracta: tienen aplicaciones directas en distintas áreas. Desde describir el movimiento de un objeto hasta optimizar recursos o diseñar gráficos digitales, su uso es clave en la vida real:
En física: velocidad instantánea y aceleración
Con la derivación podemos pasar de una posición a una velocidad y luego a una aceleración. Así, la física se apoya en el cálculo para predecir movimientos y trayectorias.
En economía: tasas de cambio y optimización
Los economistas usan derivadas para hallar mínimos y máximos de costos o ingresos. Con este análisis podemos resolver problemas de eficiencia y optimización de recursos.
En tecnología: modelación de funciones y gráficos
Las funciones matemáticas se utilizan en software, gráficos por computadora y modelación de procesos. A menudo se recurre a integración y derivación para calcular áreas, curvas y representaciones en 3D.
Recursos para profundizar en el estudio de límites y derivadas
Aprender límites y derivadas requiere práctica constante y buenas fuentes de apoyo. Hoy en día contamos con materiales accesibles y dinámicos que facilitan la comprensión de estos temas en el cálculo. Aquí te compartimos algunos recursos clave:
Libros y manuales recomendados
Los grandes matemáticos como Newton y Leibniz dieron origen a la derivación y la integración. Actualmente, existen manuales modernos en formato PDF que explican desde la definición de límites más sencilla hasta problemas complejos con ejercicios de límites y derivadas resueltos.
Muchos de estos textos incluyen teoría clara, ejemplos aplicados y ejercicios con soluciones paso a paso, ideales para estudiantes que desean avanzar de forma autónoma.
Herramientas visuales y simuladores interactivos
Las plataformas digitales permiten resolver problemas con apoyo visual. Con estos simuladores puedes ver cómo cambia la pendiente de una curva, analizar el comportamiento de una función continua o comprobar el resultado de una integral.
Además, muchos incluyen prácticas con fracciones (frac), aproximaciones con lim, situaciones que tienden a infinito o gráficos en 3D que muestran la relación entre las variables. Esto hace que el aprendizaje sea más intuitivo y atractivo.
Lecciones de cálculo con Superprof Chile
Una de las mejores formas de avanzar con seguridad es contar con la guía de un docente. En Superprof Chile puedes encontrar expertos en cálculo, límite, derivadas e integrales que adaptan sus sesiones a tu nivel y necesidades. Con explicaciones personalizadas, ejemplos prácticos y apoyo constante, el progreso es mucho más rápido y sólido que estudiando solo. ¿Y lo mejor? Sesiones 100% adaptadas a cada estudiante, para que vayas con un aprendizaje a tu propio ritmo. Anímate a tomar tu primera lección gratis.
Consejos para mejorar la comprensión progresiva
🌱 Comienza con lo esencial: domina primero las definiciones básicas para no abrumarte con demasiada teoría.
📊 Aprende con ejemplos paso a paso: resolver casos sencillos te dará seguridad antes de abordar problemas abstractos.
✍️ Usa la notación con precisión: escribir bien cada límite, derivada o integral evita confusiones y errores comunes.
🔄 Refuerza con variedad de ejercicios: combina teoría con aplicaciones en física, economía o tecnología para una comprensión más completa.
Conclusión: dominar los límites y derivadas es posible
Verás que con esta guía completa y habiendo puesto a prueba esta combinación de teoría, práctica guiada y apoyo, cualquier estudiante puede fortalecer su dominio del análisis matemático y sentirse más seguro al trabajar con funciones, derivadas e integrales.
Así que, ¡tranquilo! La mejor manera de avanzar es practicar con ejercicios que combinen funciones lineales, cuadráticas, integrales y análisis de continuidad. Con ayuda de un tutor en Superprof Chile, podrás resolver dudas específicas y fortalecer tu confianza paso a paso.
Síntesis del artículo
¡Ya lo sabes! Los límites y las derivadas son el corazón del cálculo. Permiten comprender cómo cambian las funciones, calcular pendientes, optimizar recursos y analizar fenómenos en distintas ciencias. Con ejemplos, ejercicios y aplicaciones reales, hemos visto cómo estos conceptos son esenciales para el análisis matemático y su conexión con la vida cotidiana.
Verás que tomando tus lecciones particulares de cálculo, sumado a la práctica constante y por supuesto, el apoyo de recursos como los que hemos visto, incluyendo cursos online matemáticas, ¡cualquier estudiante pueda dominar estos conceptos matemáticos con éxito!
Resumir con IA: