Dominar las operaciones con raíces cuadradas es una habilidad clave en la educación secundaria y en muchas áreas del conocimiento. No se trata solo de aplicar fórmulas o reglas, sino de comprender cuándo y cómo utilizarlas correctamente.
Es por ello, que en este artículo abordamos paso a paso las principales operaciones con raíces cuadradas, sus condiciones, errores comunes, ejercicios para practicar ¡y mucho más! Así, podremos entender paso a paso la suma, resta, multiplicación y división de raíces cuadradas, con ejemplos y ejercicios resueltos ideales para estudiantes de enseñanza media y preparación PSU en Chile:
¿Qué son las operaciones con raíces y por qué son importantes?
Las operaciones con raíces cuadradas consisten en sumar, restar, multiplicar o dividir expresiones que contienen raíces. Estas operaciones permiten simplificar cálculos, resolver ecuaciones y analizar funciones más complejas. A diferencia de una potencia, donde se eleva un número a un exponente, la raíz cuadrada representa la operación inversa de una potencia de exponente 2.
¿Cuándo se aplican en la vida académica y cotidiana?
En las matemáticas escolares, estas operaciones aparecen al simplificar expresiones algebraicas, resolver ecuaciones cuadráticas, y calcular áreas o longitudes. Más allá del aula, estas operaciones aparecen en múltiples situaciones:
- Geometría: calcular longitudes usando el teorema de Pitágoras.
- Física: en fórmulas que involucran velocidad o aceleración.
- Estadística: en el cálculo de la desviación estándar.
- Finanzas: para calcular tasas de crecimiento promedio.
Por eso, saber multiplicar, sumar, restar o dividir raíces cuadradas no es solo un ejercicio académico, sino una herramienta de análisis en contextos reales.
¿A qué nos referimos? Ahora, pongamos de ejemplo que, deseamos conocer la longitud de un lado de una losa cuadrada de 36 m².
Para ello, realizas la operación √36, lo que da como resultado 6 metros. Así, aplicas directamente una función raíz con utilidad real. ¡Las mates nos rodean en nuestro día a día!
Y no tienen porqué ser una pesadilla...
Descubre algunos métodos prácticos para aprender a calcular la radicación fácilmente ¡en todas tus operaciones matemáticas!
Suma y resta de raíces cuadradas
Aunque parezcan simples, estas operaciones tienen condiciones específicas para aplicarse correctamente. Así que, ¡muy atento aquí! Porque estás a punto de aprender a sumar y restar raíces cuadradas, lo cual es posible únicamente cuando se trabaja con raíces semejantes, es decir, aquellas que comparten el mismo radicando.
Condición clave: raíces semejantes
Para poder sumar o restar raíces cuadradas, los radicandos (los números dentro del signo radical) deben ser iguales. En este caso, hablamos de raíces semejantes.
📘 Ejemplo válido:
√2 + √2 = 2√2
📘 Ejemplo que no se puede simplificar:
√3 + √2 (no son semejantes, no se pueden sumar directamente)
Suma de raíces: ejemplos y pasos
¿Los radicandos son iguales? Si lo son, suma los coeficientes externos.
📘 Ejercicio:
3√5 + 2√5 = (3 + 2)√5 = 5√5
Ambos términos tienen √5 como radical común, así que simplemente se suman los coeficientes:
Resultado: 5√5
📘 Ejercicio:
√50 + √8
√50 = √(25×2) = 5√2
√8 = √(4×2) = 2√2
Resultado: 7√2
Resta de raíces: cómo resolverla
La lógica es la misma que para la suma. Solo puedes restar si las raíces son semejantes.
📘 Ejercicio:
6√7 - 2√7 = 4√7
Si no lo son, intenta descomponer los radicandos en factores cuadrados para verificar si se pueden simplificar.
📘 Ejemplo:
√18 - √8
√18 = 3√2
√8 = 2√2
Resultado: 3√2 - 2√2 = √2
Multiplicación de raíces cuadradas
La multiplicación de raíces cuadradas se basa en una propiedad fundamental de los radicales. Permite transformar productos complejos en expresiones más simples con un solo radical.
Pero antes, ¿qué es y para que sirve la raíz cuadrada?
Regla: √a × √b = √(a × b)
Esta regla se aplica para cualquier par de números reales positivos o cero.
📘 Ejemplo paso a paso:
√3 × √12 = √(3 × 12) = √36 = 6
Este tipo de multiplicación de raíces es muy útil para reducir expresiones algebraicas con radicales.
Multiplicación con números enteros y raíces
También se puede multiplicar un número entero por una raíz:
Ejemplo mixto:
2√5 × 3√2 = (2 × 3)(√5 × √2) = 6√10
Se multiplican los coeficientes y luego los radicandos.
División de raíces cuadradas
La división es otra de las operaciones con raíces fundamentales, y puede aplicarse siempre que el denominador sea diferente de cero.
Regla: √a / √b = √(a / b)
📘 Ejemplo simple:
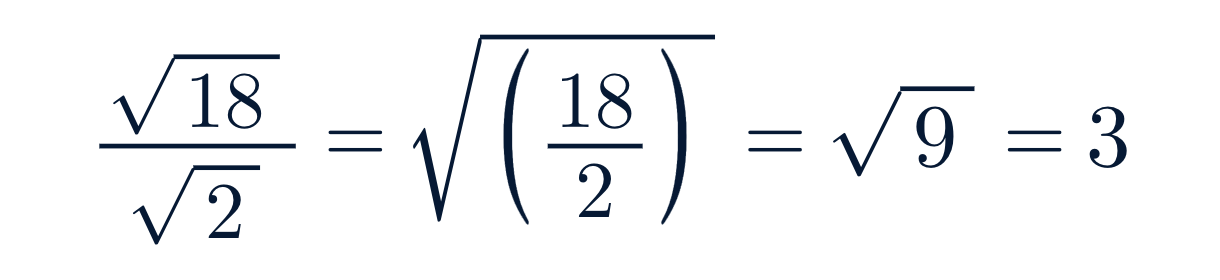
Este método permite resolver fracciones con raíces sin complicaciones.
Racionalización de raíces
Cuando una raíz cuadrada aparece en el denominador, se debe racionalizar. Esto significa eliminar el radical multiplicando numerador y denominador por una raíz que elimine la del denominador.
📘 Ejemplo clásico:
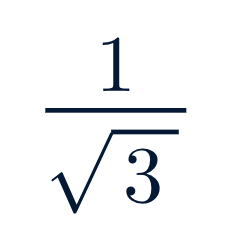
Multiplicamos por √3 arriba y abajo:
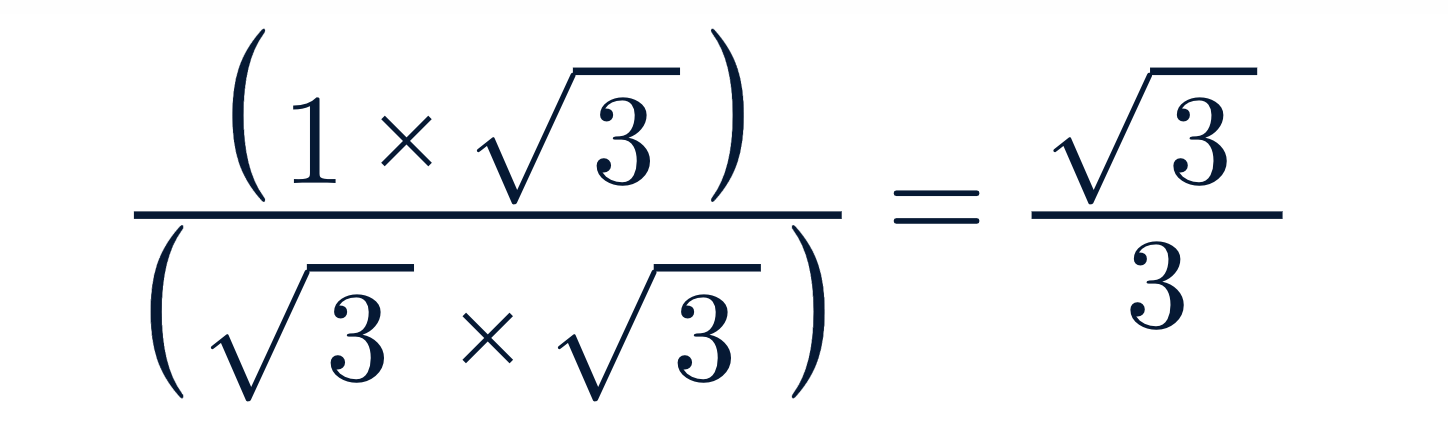
Operaciones combinadas con raíces cuadradas
A menudo, las expresiones con radicales requieren aplicar varias operaciones al mismo tiempo. En estos casos, se sigue el orden de operaciones o regla PEMDAS (Paréntesis, Exponentes, Multiplicación/División, Suma/Resta).
¿Cómo resolver expresiones con varias operaciones?
📘 Ejemplo combinado:
2√3 + √12 - √3
Paso 1: Simplificamos raíces si es posible.
√12 = √(4 × 3) = 2√3
Entonces:
2√3 + 2√3 - √3 = (2 + 2 - 1)√3 = 3√3
Aquí sumamos y restamos raíces semejantes tras simplificarlas.
Casos especiales y errores comunes al operar con raíces
A continuación, te compartimos algunos de los errores frecuentes que cometen los estudiantes al trabajar con operaciones combinadas o propiedades de radicales. ¡Mucha atención a estos detalles!
Evitar errores con raíces no semejantes
No confundas la suma de raíces con la raíz de una suma.
Error común:
√(9 + 16) = √25 = 5
❌ No es igual a: √9 + √16 = 3 + 4 = 7
✅ Lo correcto es:
Solo puedes sumar o restar raíces si son semejantes, es decir, si tienen el mismo radicando. En este caso, al no ser semejantes, no se pueden combinar directamente.
√(a + b) ≠ √a + √b
Recuerda: Siempre verifica si las raíces tienen el mismo radicando antes de operar.
Confusión con signos negativos
No se puede calcular la raíz cuadrada de un número negativo dentro del conjunto de números reales. Si lo intentas, obtendrás un número complejo.
📌 Error común:
√(-4) ❌ no tiene solución real
¿Quieres aprender a calcular correctamente los números negativos?
✅ Lo correcto es:
√(-4) = 2i → este resultado pertenece al conjunto de números imaginarios, y se estudia más adelante, al trabajar con funciones complejas.
Consejo: Si el radicando es negativo, detente: en las matemáticas básicas, la raíz no está definida. Revisa si hay una forma de reescribir o transformar la expresión antes de continuar.
Tabla resumen con las propiedades más importantes
Esta tabla es una herramienta esencial para estudiantes de enseñanza secundaria o quienes están comenzando con el análisis de funciones y operaciones con raíces cuadradas. Resume las principales propiedades que rigen la radicación y muestra cómo aplicarlas correctamente con ejemplos numéricos.
| Propiedad | Fórmula | Ejemplo |
|---|---|---|
| Producto | √(a × b) = √a × √b | √(4 × 9) = √4 × √9 = 2 × 3 = 6 |
| Cociente | √(a / b) = √a / √b | √(16/25) = 4/5 |
| Potencia par | √(a²) = |a| | √((-5)²) = √25 = 5 |
| Igualdad | √a = √b ⇒ a = b | √x = √49 ⇒ x = 49 |
| Simplificación | √(ab) = √a × √b (con factor) | √72 = √(36 × 2) = 6√2 |
¿Te gustaría repasar estas propiedades del radicando? Domínalas todas ellas con esta guía y ejercicios prácticos.
Verás que aprender estas reglas ¡será lo mejor! ya que te permiten simplificar expresiones, resolver ecuaciones con radicales y trabajar con fracciones y radicandos complejos de manera ordenada. Memorizar estas fórmulas y saber aplicarlas correctamente, facilita el reconocimiento de errores comunes y mejora el rendimiento en pruebas.
¿Cómo aplicar estas propiedades en ejercicios reales?
Dominar las propiedades de la raíz cuadrada implica saber cuándo y cómo aplicarlas. Aquí presentamos tres ejercicios resueltos que te permitirán afianzar lo aprendido paso a paso. Estos casos combinan suma, multiplicación, división y simplificación de radicales, aplicando técnicas como la descomposición en factores y el reconocimiento de raices semejantes.
📝 Ejercicio 1: Simplificación de raíces
Planteamiento
Simplificar la expresión:
√50 + √8
Solución paso a paso:
Descomponemos cada radicando en factores que contengan cuadrados perfectos:
√50 = √(25 × 2) = √25 × √2 = 5√2
√8 = √(4 × 2) = √4 × √2 = 2√2
Ahora sumamos:
5√2 + 2√2 = 7√2
Resultado final:
7√2 es la forma simplificada. Solo pudimos operar porque ambas raíces eran semejantes (tenían el mismo radicando: 2).
📝 Ejercicio 2: Igualación de raíces
Planteamiento
Resolver la ecuación:
√x = √36
Solución paso a paso:
Aplicamos la propiedad de igualdad de raíces (si √a = √b, entonces a = b):
√x = √36
⇒ x = 36
Resultado final:
x = 36
Este tipo de ecuaciones con radicales se resuelve fácilmente si los índices son iguales y las raíces están definidas en el conjunto de números reales.
📝 Ejercicio 3: Expresión combinada
Planteamiento
Resolver:
√(9/16) × √4
Solución paso a paso:
Primero operamos cada raiz:
√(9/16) = √9 / √16 = 3 / 4
√4 = 2
Multiplicamos ambas fracciones:
(3/4) × 2 = 3/2
Resultado final:
3/2
Este ejercicio combinó división de raíces, radicandos fraccionarios y multiplicación, todo con aplicación directa de las propiedades.
Practicar ejercicios de raíz cuadrada fortalece habilidades como identificar cuadrados perfectos, usar correctamente el índice y radicando, y aplicar reglas de multiplicación y racionalización. Estos contenidos son clave en la PSU y pruebas técnicas, mejorando tu rendimiento en matemáticas.
Síntesis del texto
Dominar las operaciones con raíces cuadradas es clave en el estudio de la matemática escolar y el álgebra básica. Saber sumar, restar, multiplicar y dividir radicales no solo permite resolver ejercicios más rápido, sino también entender mejor temas como funciones, potencias y ecuaciones. Aplicar correctamente cada propiedad y evitar errores comunes facilita un aprendizaje más sólido.
Si estás en Chile y quieres reforzar estos contenidos, Superprof Chile te ofrece profesores especializados en raíces cuadradas, potencias, álgebra y funciones. Con lecciones 100% personalizadas, podrás dominar estas operaciones y avanzar con confianza en tus estudios.
No lo postergues más y empieza a potenciar tus habilidades con los números, tomando tu primera lección gratis junto al superprofe ¡que tú mismo elijas! Inicia hoy con las mejores sesiones presenciales, online o a domicilio, disponible en todas las comunas y ciudades del país...
¿Te gustó este artículo? ¡Evalúalo!
Loading...
