Los números racionales están presentes en nuestra vida diaria más de lo que se piensa ¿No nos crees?: ¿Qué números ocupamos cuando tenemos que calcular 3/4 de litros de leche? o ¿Cómo determinamos cuánto es el 25% de descuento de un precio? Todas estas operaciones se basan en el manejo de números racionales.
En este artículo aprenderemos más sobre este grupo numérico, y entenderemos, mediante diferentes ejercicios, cómo se realiza la multiplicación y división de números racionales, y cómo la podemos utilizar en nuestras labores diarias.

¿Cómo se realiza la multiplicación de números racionales?
Reglas básicas para multiplicar números racionales
Los números racionales (expresados con la letra Q) son todos los números que pueden representarse en forma de fracción. Por ejemplo:
a/b
- “a” es el numerador (tiene que ser un número entero, puede ser positivo o negativo y también puede ser cero)
- “b” es el denominador (tiene que ser un número entero que no sea cero)
Para multiplica dos fracciones lo único que se tiene que hacer es multiplicar numerador por numerador y denominador por denominador. Veamos el siguiente ejemplo:
3/4 x 4/7 = 3x4; 4x7 =12/28
Este resultado lo podemos simplificar por el máximo común divisor de ambos números que en este caso sería el número 4. El resultado entonces es: 3/7.
Ahora, hay que tener en cuenta que la multiplicación de fracciones también se ve sujeta a las reglas de los signos, llámense positivo o negativo. Recordemos estas reglas:
- (+ × +) = +
- (+ × –) = –
- (– × +) = –
- (– × –) = +
Veamos estos dos ejemplos:
3/4 x -2/5= 3 x -2; 4 x 5= -6/20
El máximo común divisor de ambos números es 2, así que simplificada esta fracción daría como resultado:
3/10
Pero ¿para qué hay que simplificar?: Simplificamos las fracciones para poder operar mejor y para evitar errores. Las cifras más grandes siempre complican los cálculos.
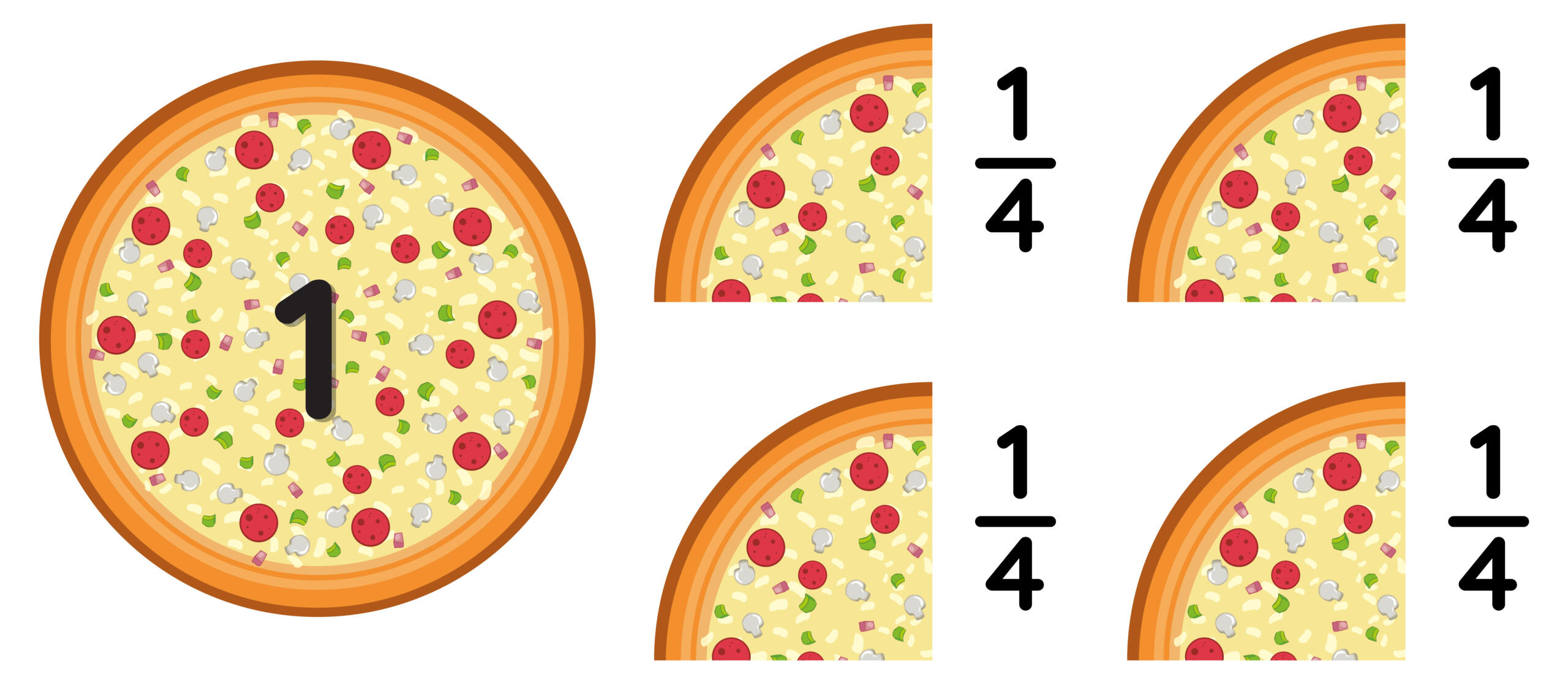
Para simplificar una fracción debemos dividir el numerador y denominador por su Máximo Común Divisor (MCD), que es el número más grande que puede dividir a cada una de las cifras.
Multiplicación y división de números racionales: ejemplos básicos
Revisemos a continuación diferentes casos donde podemos multiplicar números racionales.
¿Cómo harías la multiplicación de números racionales de este tipo?
31/2 x 2/3
La primera fracción está encabezada por el número entero 3. A estas cifras se les conoce como números mixtos, y para operar con ellas deben ser transformadas a fracciones.
Esta modificación se hace de la siguiente forma: se multiplica el número entero por el denominador y se le suma el numerador. O sea, multiplicamos el 3 por el 2 y le sumamos el 1.
El resultado sería una fracción impropia (donde el numerador es mayor al denominador)
3 x 2 + 1/2= 7/2
El resultado de la multiplicación sería entonces:
7/2 x 2/3= 14/6
Ahora, si multiplicamos cifras que son decimales exactos debemos hacerlo de la siguiente forma. Revisemos este ejemplo:
0.5 × 0.2 = 0.10
O podemos transformar estas cifras con decimales a fracciones. Por ejemplo, el 0,5 es lo mismo que decir 1/2, y 0,2 es igual que decir 1/5. Entonces, hacemos la multiplicación.
1/2 x 1/5= 1/10
División de números racionales
Regla del inverso multiplicativo
Para poder hacer la división de racionales también hay que multiplicar. Te lo explicamos: Cuando se dividen dos fracciones hay que multiplicar de manera cruzada ambas cifras.
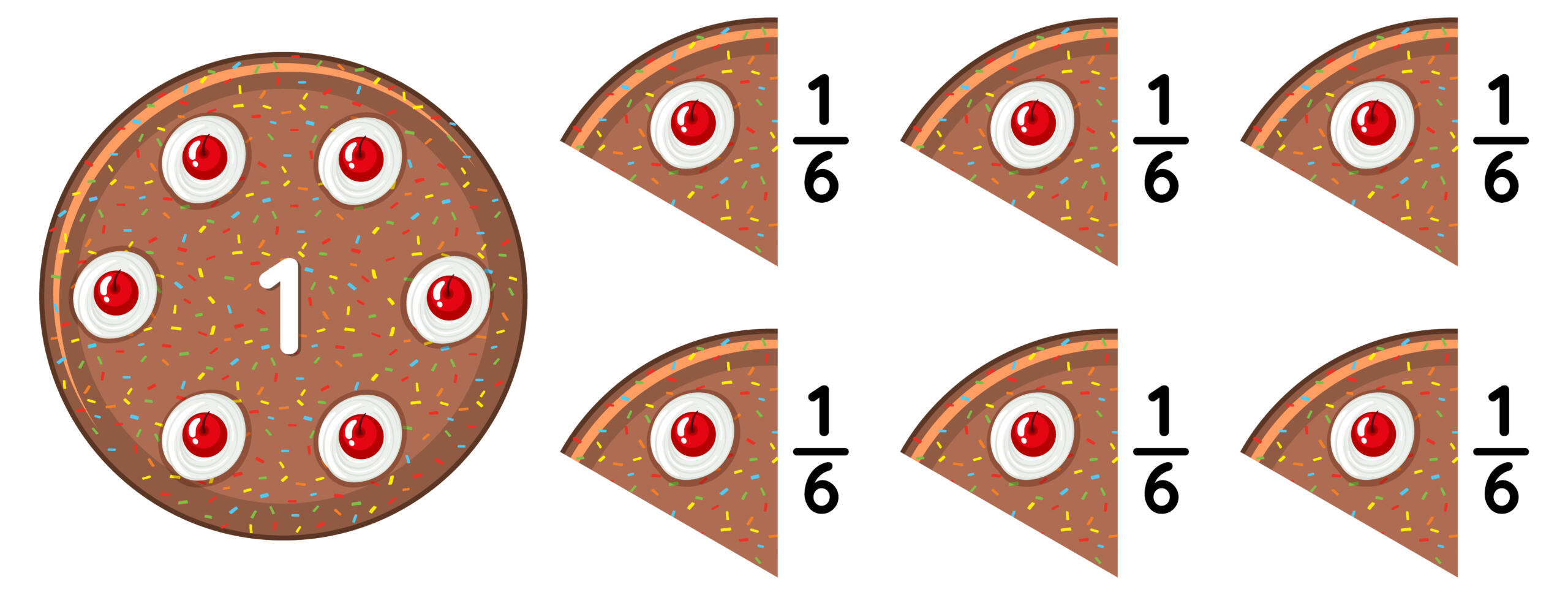
Ejemplo:
2/3: 3/7
Lo que hay que hacer a continuación es multiplicar cruzado, o sea se multiplica el 2x7 y el 3x3, de la siguiente forma:
2/3 ÷ 3/7= 2 x 7; 3 x 3= 14/9.
Más ejemplos de división de números racionales
Ahora dividamos las siguientes cifras:
0,25 ÷ 3/4
La cifra 0,25 es lo mismo que decir 25/100, que simplificado sería 1/4. Entonces, la división quedaría de la siguiente forma:
1/4 ÷ 3/4= 1 x 4; 4 x 3 = 4/12
Simplificado quedaría 1/3.
Interpretar ejercicios de multiplicación y división de números racionales
Los números racionales (fracciones o números con decimales) son la representación matemática de las partes de un todo, divisiones que siempre están presente en la vida real.
Significado matemático y visual de estas operaciones
Para entender mejor cuál es la ubicación y la función de un número racional debemos saber ubicarlo en una recta numérica. Entendamos, entonces, esta multiplicación en la recta numérica:
2/3 x 3
Esto significa que debes avanzar 3 veces 2/3 en la recta numérica. La primera posición será, entonces, 2/3; la segunda posición será 4/3 y la tercera posición será 6/3. Por ende, el resultado es 2.
Ahora veamos la división:
2 ÷ 1/2
La incógnita de esta operación es cuánto cabe 1/2 en 2. Ahora imagina la recta numérica entre el cero y el 2. Recuerda que 1/2 también equivale a 0,5.
La primera posición en la tabla es 1/2, la segunda posición sería 1, la tercera sería 3/2 y la cuarta sería 2. Entonces, pudimos dar 4 saltos desde 0 a 2. Por ende 2 ÷ 1/2 es igual a 2.
¿Cómo aplicar los números racionales en la vida diaria?
En las recetas
Imagina tienes una receta que te pide poner en esta 3/4 de una taza de azúcar. Pero tú no quieres hacer toda la receta, vas a hacer solo la mitad, por ejemplo, un queque más pequeño. ¿Cómo lo solucionas?
Lo que tienes que hacer es dividir 3/4 ÷ 2.
3/4 ÷ 2= 3x1; 4x2 = 3/8.
El resultado es 3/8, o sea que debes ocupar solo un 3/8 de azúcar. Y eso equivale a dividir la taza en 8 partes y solo ocupar 3.
Descubre en este artículo todo sobre las aplicaciones de los números racionales en la vida real.
Al ir a comprar
Imagina vas al mall y ves una polera que te gusta y que tiene un descuento. La polera cuesta $12000 y tiene un descuento de 25%. ¿Qué harías para calcular el descuento en peso que tiene la polera?

Decir 25% es lo mismo que decir 25/100, que simplificado es 1/4. Entonces para sacar el valor del descuento debemos multiplicar $12000 por 1/4.
12000 x 1/4 =3000.
El descuento que están haciendo a la polera es de $3000.
Consejos para dominar la multiplicación y división de números racionales
Errores comunes en multiplicación y división de números racionales
No respetar el mismo denominador
En la suma y en la resta, las fracciones deben tener el mismo denominador. La adición y sustracción de números racionales sin el mismo denominador es un error grave.
No simplificar
A veces el trabajo con fracciones puede arrojar cifras bastante altar, como por ejemplo 75/200. Estas fracciones se pueden simplificar para poder multiplicar o dividir de mejor manera y no enredarse en el intento. En este caso la fracción 75/200 simplificada quedaría 3/8.
No tomar en cuenta los signos (+ y -)
Si no tomas en cuenta las reglas que rigen los signos positivos y negativos el resultado de las fracciones siempre será incorrecto.
No transformar decimal a fracción
Para operar con fracciones las dos cifras deben ser fracciones. Es incorrecto operar números con decimales con fracciones. Siempre hay que generar la equivalencia.
Recursos para practicar y mejorar
Los buenos nuevos tiempos ofrecen varias ventajas, sobre todo en lo que respecta al uso de la tecnología. Si aún te cuesta los números racionales puedes ayudarte con aplicaciones, las que te guiarán paso a paso. Entre las App gratuitas que puedes encontrar están:
- Photomath.
- Khan Academy.
- Brilliant.org.
Ahora, si aún tienes problemas para entender la matemática de las fracciones y sus operaciones combinadas con números racionales lo mejor que puedes hacer es conseguir un profesor particular.
Para elegir dentro de una gama amplia de tutores de educación personalizada puedes ingresar al portal de Superprof y escoger al que más se ajuste a tus intereses académicos. Por ejemplo, en Osorno, hay excelentes profesores matemáticas disponibles.
Síntesis del artículo
En este artículo revisamos varios ejercicios de multiplicación y división de números racionales y aprendimos cómo resolverlos.
También repasamos las reglas elementales para transformar decimales a fracciones, y supimos cómo estas cifras se aplican a la vida real a través de diferentes situaciones.
Recuerda siempre que los números racionales y sus matemáticas son un aliado, no un enemigo. Saber utilizarlas te facilitará la vida y te sacará de muchos problemas.
Si requieres apoyo adicional, consulta a profesores matemáticas en tu localidad.
Resumir con IA:















