¿Sabías que puedes calcular una raíz cuadrada sin usar una calculadora? Aunque hoy muchas personas dependen de dispositivos electrónicos para resolver este tipo de cálculos, existen métodos manuales que siguen siendo muy útiles.
En este artículo aprenderás paso a paso cómo hallar raíces cuadradas con distintos enfoques: desde la descomposición en factores primos hasta el método del promedio usado por los babilonios. ¡Ideal para estudiantes, docentes y entusiastas de las matemáticas!
Pero antes, ¿qué es una raíz cuadrada y para qué sirve?
¿Por qué es útil saber calcular raíces cuadradas a mano?
En la era digital, puede parecer innecesario aprender a resolver una raíz cuadrada a mano, pero las ventajas son muchas. A continuación, te mostramos por qué este conocimiento sigue siendo relevante:
Ventajas de no depender de una calculadora
- Refuerza el pensamiento lógico y la comprensión del proceso detrás del resultado.
- Es útil durante pruebas escritas, donde a veces no se permite el uso de dispositivos.
- Ayuda a simplificar cálculos mentales en situaciones cotidianas.
- Facilita la comprensión de otros temas como el álgebra, los números enteros y las fracciones.
- Permite entender la relación entre cuadrado y raíz cuadrada, lo que fortalece la capacidad para resolver ecuaciones y estimar valores decimales.
Partes de una raíz cuadrada explicadas paso a paso
Antes de entrar en los métodos prácticos, es importante conocer la estructura básica de una raíz cuadrada. Esto te permitirá interpretar y escribir correctamente cada parte del cálculo.
Elementos básicos de una raíz cuadrada
La expresión √x se compone de tres partes:
Signo radical (√)
También llamado símbolo de raíz cuadrada, indica que vamos a calcular el número que, al multiplicarse por sí mismo, da el valor original.
Radicando
Es el número ubicado dentro del signo radical. Es el valor del cual queremos hallar la raíz cuadrada.
Resultado
Es la cifra final que obtenemos tras aplicar el método de cálculo.
Ejemplo: En √64
Signo radical: √
Radicando: 64
Resultado: 8, porque 8 × 8 = 64
Conoce más de las propiedades de las raíces cuadradas ¡aquí!
Método clásico para calcular una raíz cuadrada a mano
Existen varias formas tradicionales de hallar una raíz cuadrada sin calculadora. Aquí exploraremos dos muy usados en el aula y también en exámenes.
Método de descomposición por factores primos
Este método consiste en descomponer el radicando en sus factores primos y luego agrupar en pares.
Pasos para calcular √144:
Descomponemos 144:
144 = 2 × 2 × 2 × 2 × 3 × 3
Agrupamos en pares de factores iguales:
(2 × 2) × (2 × 2) × (3 × 3)
Tomamos un número de cada par:
2 × 2 × 3 = 12
Resultado: √144 = 12
Este método es útil cuando el radicando es un cuadrado perfecto y puede simplificarse fácilmente con multiplicación entre factores primos.
Algoritmo largo o método tradicional de raíz cuadrada
Conocido como el “algoritmo de renglón” o “método del doble y producto”, este método permite hallar raíces cuadradas incluso de números grandes y decimales.
📝 Ejemplo con √529:
Agrupamos los números en pares desde la derecha. En este caso, 5 | 29
Buscamos el número que elevado al cuadrado se acerque a 5 → 2 × 2 = 4
Escribimos el 2 en el resultado y restamos: 5 – 4 = 1
Bajamos el siguiente par: 129
Doblamos el resultado parcial (2 × 2 = 4) y lo escribimos como primer dígito del nuevo divisor. Probamos con cifras hasta encontrar la que se ajusta (en este caso, 3).
El resultado es 23, porque 23 × 23 = 529
Este algoritmo es muy útil cuando queremos calcular raíces sin calculadora y no conocemos los factores primos del número.
Cómo sacar la raíz cuadrada fácilmente con aproximaciones
Cuando el radicando no es un cuadrado perfecto, puedes usar técnicas de estimación para obtener un resultado cercano. Aquí veremos dos estrategias efectivas.
Redondeo con cuadrados perfectos cercanos
Una forma rápida de hallar raíces cuadradas aproximadas es ubicar el número entre dos cuadrados perfectos.
Ejemplo con √50:
Sabemos que √49 = 7 y √64 = 8
Como 50 está más cerca de 49, estimamos que √50 ≈ 7,1
Si queremos mayor precisión, usamos decimales intermedios.
Este método es útil para estimar cifras mentalmente, sobre todo si el número no tiene una raíz exacta.
Para los pitagóricos, encontrar números como √2 fue tan desconcertante que llegaron a ocultarlos por considerarlos "irracionales" (1,4142...). En cambio, los babilónicos desarrollaron métodos para hallar raíces cuadradas precisas (incluso decimales), usando solo promedios simples y divisiones.
Método del promedio o método babilónico
Este antiguo método consiste en tomar una estimación inicial y mejorarla en cada paso usando promedios.
Ejemplo con √20:
Supón que la raíz cuadrada de 20 es 4,5
Divide: 20 / 4,5 ≈ 4,44
Promedia: (4,5 + 4,44) / 2 ≈ 4,47
Repite si quieres más exactitud
Este método se basa en la idea de que el promedio entre una estimación y el resultado inverso se acerca progresivamente al valor real. Es rápido y puede hacerse en 2-3 pasos mentales o en papel.
Herramientas de apoyo: tabla de raíces cuadradas y tips mentales
Tener recursos visuales y estrategias mentales ayuda a resolver raíces cuadradas de forma más ágil. Aquí te compartimos algunas:
Tabla raíz cuadrada de los primeros 30 números
| Número | Raíz cuadrada |
|---|---|
| 1 | 1 |
| 2 | 1,41 |
| 3 | 1,73 |
| 4 | 2 |
| 5 | 2,23 |
| 6 | 2,45 |
| ... | ... |
| 25 | 5 |
| 30 | 5,47 |
Esta tabla sirve como referencia rápida para estimar raíces cuadradas sin necesidad de calculadora, especialmente cuando trabajas con decimales.
Ahora, ¿qué pasa con los números negativos? Aprende a aplicarles raíces cuadradas.
Trucos mentales y atajos comunes
Cuando no tienes una calculadora a mano o necesitas hacer un cálculo rápido, algunos trucos mentales pueden ayudarte a hallar la raíz cuadrada de un número o, al menos, a saber si es un cuadrado perfecto. Aquí te mostramos estrategias sencillas para reconocer patrones y simplificar el proceso:
🔢 1. ¿El número es un cuadrado perfecto? Fíjate en la última cifra
Un truco rápido para saber si un número podría tener una raíz cuadrada exacta es observar su última cifra. Los números cuadrados perfectos nunca terminan en 2, 3, 7 u 8.
Esto significa que si ves un número como 58, 93 o 77, puedes descartar que tenga una raíz exacta sin hacer el cálculo completo.
Ejemplos de cuadrados perfectos y sus terminaciones:
- √49 = 7 → termina en 9
- √64 = 8 → termina en 4
- √81 = 9 → termina en 1
- √100 = 10 → termina en 0
✅ Terminaciones posibles en cuadrados perfectos: 0, 1, 4, 5, 6 o 9
❌ Si termina en 2, 3, 7 u 8, la raíz cuadrada no es exacta
📉 2. Para fracciones, simplifica raíz por separado
Cuando trabajas con fracciones, puedes separar el numerador y el denominador para simplificar la raíz cuadrada:
Ejemplo:
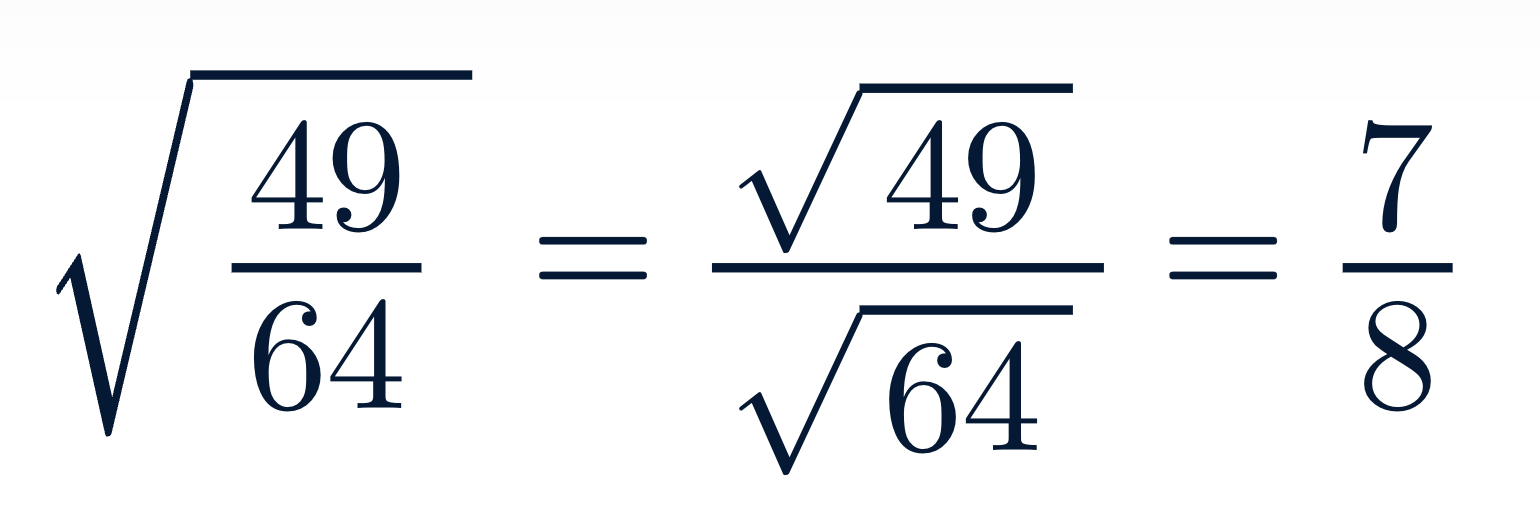
Este truco funciona siempre que ambas cifras sean cuadrados perfectos. Si no lo son, puedes intentar convertirlos a decimales y luego aplicar el método del promedio o una estimación.
También es útil recordar que:
√(1/4) = 1/2
√(9/16) = 3/4
√(25/100) = 5/10 = 0,5
Este método permite resolver raíces cuadradas con fracciones sin necesidad de memorizar fórmulas complejas.
🧮 3. ¿Tiene ceros al final? Usa la coma decimal correctamente
Si el número tiene cifras pares de ceros al final (como 100, 400, 900), puedes separarlos y calcular la raíz como si trabajaras con decimales:
Ejemplo:
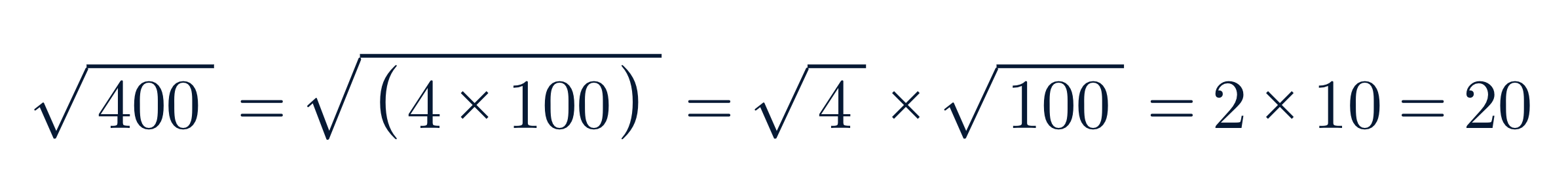
Este mismo truco se puede aplicar con decimales, moviendo la coma dos posiciones por cada par de ceros:
Ejemplo con decimal:
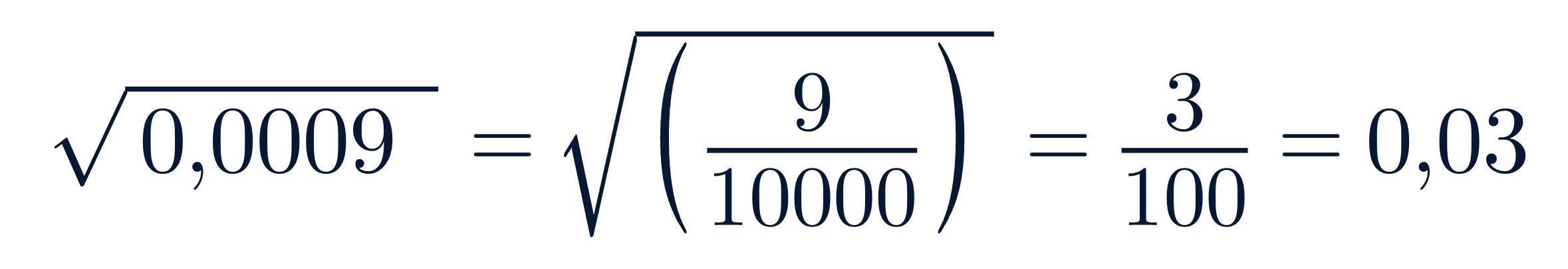
Esto se debe a que cada par de ceros en el radicando equivale a mover la coma decimal una posición en la raíz cuadrada. Es útil en cálculos financieros, científicos y escolares donde hay que obtener valores exactos o redondeados.
¿Cómo calcular raíces cuadradas con decimales o fracciones?
Aprender a calcular raíces cuadradas de decimales y fracciones amplía tu comprensión de funciones numéricas y permite resolver problemas más complejos.
Raíces cuadradas de decimales
Cuando el radicando tiene coma decimal, puedes mover la coma dos lugares hacia la derecha (como si multiplicaras por 100), calcular y luego volver a colocarla.
Ejemplo:
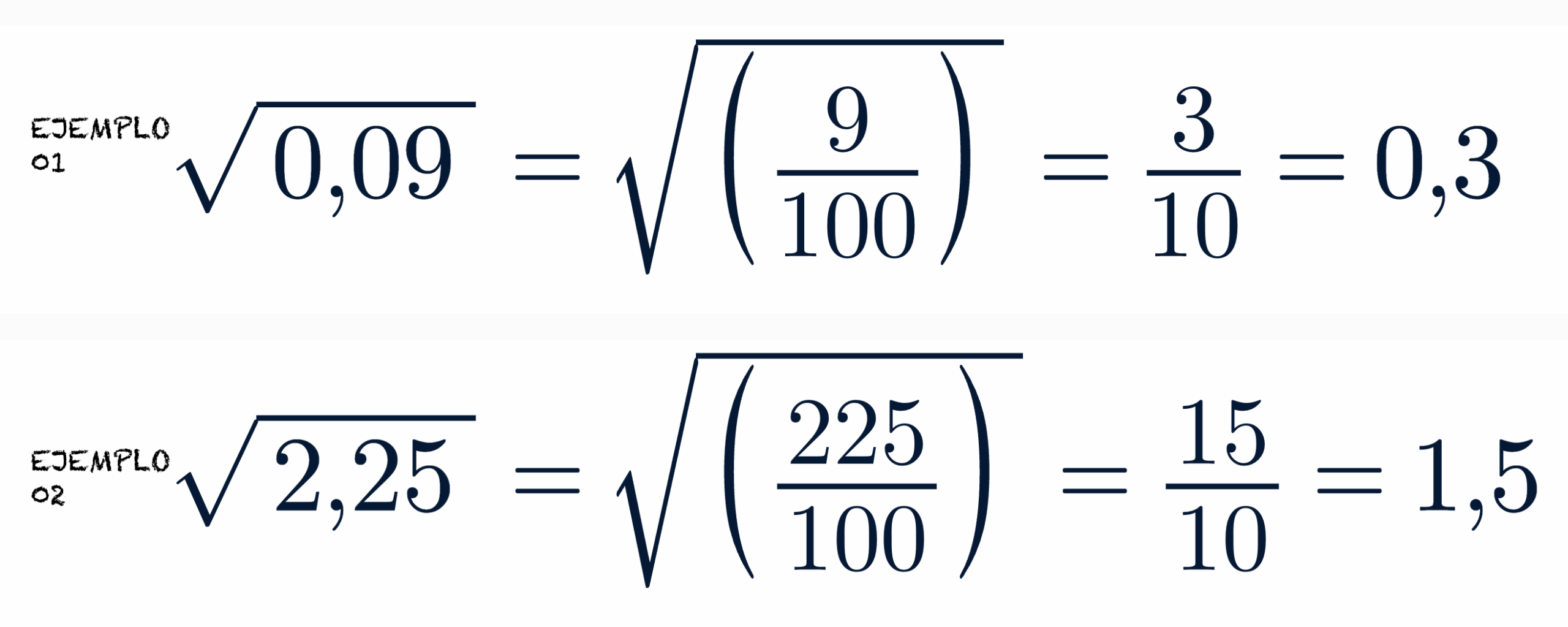
Raíces cuadradas de fracciones
La regla general es aplicar la raíz por separado al numerador y al denominador.
Ejemplo:
√(1/4) = √1 / √4 = 1/2
√(9/16) = 3/4
También puedes convertir a decimales, aplicar el cálculo y simplificar el resultado final si es necesario.
¿Quieres practicar con más ejemplos? Encuentra un talonario guía ¡aquí!
Síntesis del artículo
Aprender a calcular raíces cuadradas sin calculadora es una habilidad muy valiosa, tanto en el aula como en la vida diaria. Ya sea mediante el método de descomposición, el algoritmo tradicional, o técnicas como el promedio babilónico, dominar estos procedimientos mejora tu agilidad mental y comprensión de cifras, decimales, fracciones y operaciones con números enteros o complejos.
Si estás en Chile y buscas reforzar este conocimiento, en Superprof Chile puedes encontrar profesores y profesoras personalizados que te enseñen a resolver raíces cuadradas, ecuaciones, funciones, y mucho más. Con esta ayuda, puedes avanzar a tu ritmo y superar cualquier dificultad en álgebra o cálculo. ¡Anímate a dar el siguiente paso con apoyo experto!
¿Te gustó este artículo? ¡Evalúalo!
Loading...
