Los números racionales (todos aquellos números que se pueden transformar en fracción) no son solo contenido matemático que se puede tratar en la escuela o la universidad. Estos números están presentes en nuestra vida cotidiana en una gran cantidad de contextos.
Las aplicaciones y propiedades de los números racionales pueden ser diversas. Estamos hablando que podemos encontrar fracciones tanto en una receta de cocina, como en el cálculo de un impuesto o en trabajos manuales de carpintería, por ejemplo.
En este artículo revisaremos distintos casos donde los números racionales o fracciones están presentes y descubriremos también cómo su correcto uso y método puede facilitarnos muchos aspectos de nuestra vida cotidiana. ¡Comencemos!

Ejemplos de números racionales en la vida diaria
Definición sencilla de números racionales
Antes de revisar el uso y propiedades de los números racionales y sus aplicaciones matemáticas en nuestra existencia cotidiana, revisemos qué son estos números en las ciencias matemáticas y cuáles son sus principales características.
Los números racionales son todos los números que se pueden expresar como fracción. Para que te hagas una idea rápida, la típica forma de los números racionales es la siguiente: a/b.
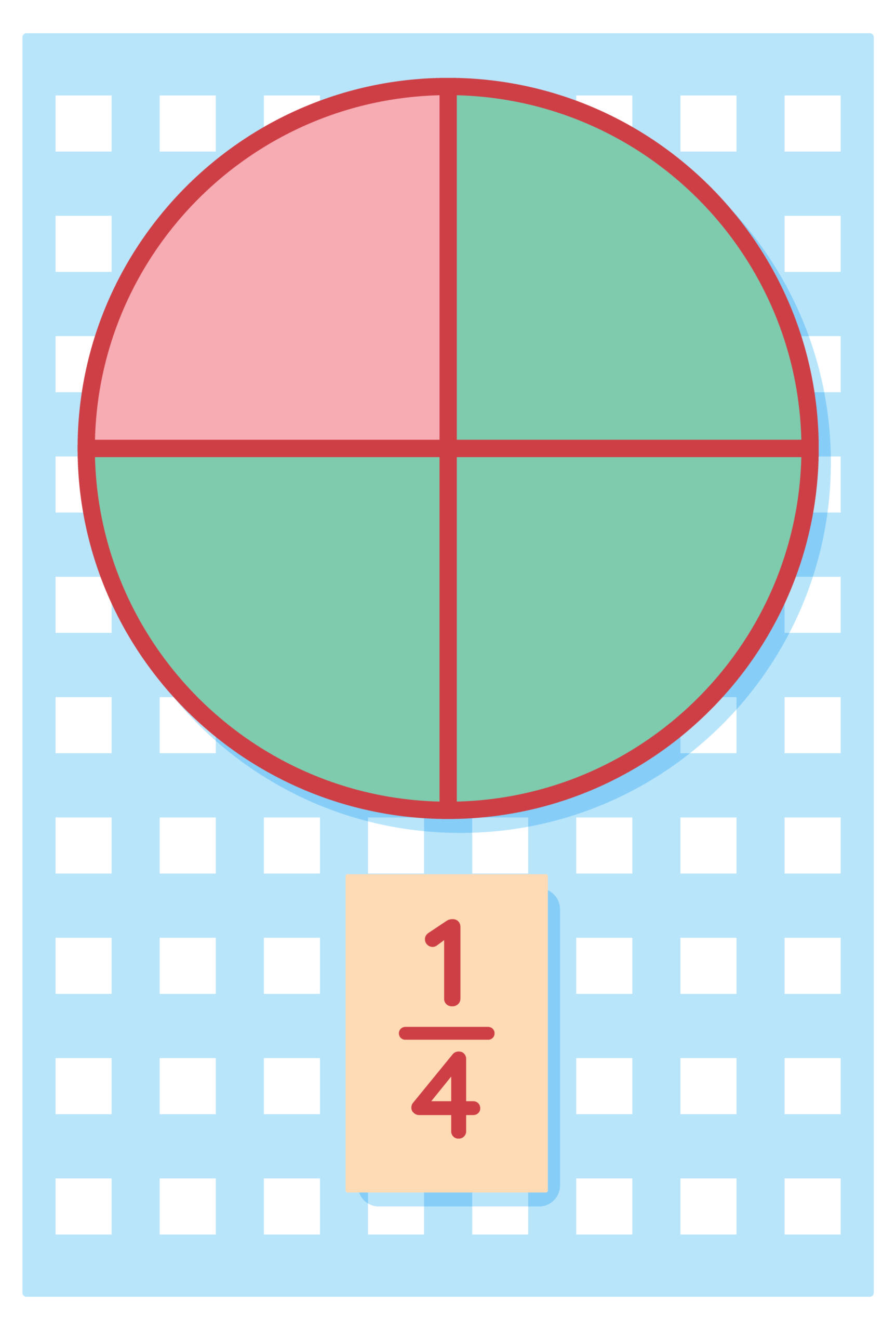
A la letra “a” se le conoce como numerador y a la letra “b” se la conoce como denominador. Todos los números enteros pueden expresarse como números racionales (el número 7 puede ser expresado como 7/1, con numerador y denominador), pero también números con decimales finitos o periódicos (infinitos) como, por ejemplo, 0,5 o el 0,333333…
Veamos esta tabla comparativa para que te quede claro la diferencia de los números racionales o fracciones con otros grupos de números:
| Conjunto de Números | Letra representativa | Descripción y propiedades |
| Números naturales | N | Estos son todos los números positivos, pero sin decimal: 0, 1, 2, 3, 4, … |
| Números enteros | Z | Estos son los números positivos, negativos e incluyen el cero: -3, -2, -1, 0, 1, 2, 3, … |
| Números racionales | Q | Fracciones o números con decimales exactos o periódicos: ½, -3, 0.75, -7/4 |
| Números irracionales | I (R/Q) | Números más complejos, como √2, π. |
| Números reales | R | Es la suma de los números racionales e irracionales. |
Para qué sirven los números racionales en contextos cotidianos
Aunque no lo creas, podemos encontrar fracciones o números racionales en todas partes. ¿Qué método ocupamos cuando queremos repartir una pizza en partes iguales? ¿a qué método recurrimos cuando queremos calcular cuál es el descuento de un producto? Ocupamos fracciones o números racionales.
Entonces, ante la pregunta ¿para qué sirven los números racionales? La respuesta es clara y directa: para entender mejor el mundo a través de las matemáticas. Además, algunos profesores matemáticas recomiendan explorar estos conceptos desde temprana edad.
¿Dónde se aplican los números racionales en la vida cotidiana?
Finanzas personales y comercio
Es increíble las aplicaciones matemáticas de los números racionales en las propiedades de nuestras finanzas y en la economía en general. Por ejemplo, usamos números racionales o fracciones para:
- Calcular un descuento.
- Dividir los gastos entre varias personas.
- Calcular cuánto te subió la cuenta de luz.
Si vas al mall y quieres comprarte una chaqueta que cuesta $90.000, pero esta tiene un 25% de descuento, tienes que ocupar fracciones y algunas operaciones de números racionales para determinar cuánto te va a salir la prenda en definitiva. Además, algunos profesores matemáticas destacan la importancia de aplicar estos conceptos en la toma de decisiones.
- Un 25% es lo mismo que decir 25/100, que simplificado quedaría 1/4.
- Entonces, hay que calcular cuánto es 1/4 de $90.000. Y eso te da como resultado $22.500.
- El descuento de la chaqueta es de $22.500.
Ahora, Imagina que vas a comer con 3 amigos y tienen que dividir la cuenta que salió $36.000. Esto significa que a cada persona le va a tocar pagar 1/3 de la cuenta, y eso es un número de $12.000 por cabeza.
Cocina y recetas
En la cocina usamos números racionales o fracciones constantemente. Las recetas suelen contener diferente información en fracciones, las que suelen determinar la cantidad de ingredientes que debemos usar en ellas.
Aunque no lo queramos vamos a tener que usar aplicaciones matemáticas y operaciones combinadas con números racionales para entender las porciones de los ingredientes a utilizar.
Mira, por ejemplo, esta receta de un queque casero con varias cifras de números racionales:
- 1 taza de azúcar.
- 2 huevos.
- 2 ½ tazas de harina sin polvos.
- 1 cucharadita de polvo de hornear.
- ½ taza de leche.
- Ralladura de limón o naranja.
Para saber cuánto es 1/2 taza de leche tenemos que aplicar un método que nos permita saber cómo operan los números racionales y sus diferentes factores. Sabemos que 1/2 es igual a 0,5, por lo tanto, nos queda claro que tenemos que ocupar la mitad de una taza de leche.
Conoce aquí todo sobre la multiplicación y división de números racionales.
Pero qué pasa si esta receta para cuatro personas se reduce a 2. ¿Qué haces con la 1/2 taza de leche que pedía originalmente la receta? Bueno, hay recurrir a las operaciones con la que operan los números racionales y reducirla a la mitad.

Tenemos 1/2 taza de leche y necesitamos dividirla en 2. La operación y el método sería el siguiente: 1/2 ÷ 2. Para resolver esta operación de números racionales tenemos que usar la multiplicación, y multiplicar cruzado 1/2 ÷ 2/1, el resultado sería 1/4.
Entonces, para hacer la receta del queque casero para dos personas necesitamos solo una fracción de 1/4 de taza de leche.
Esta es una muestra clara de operaciones usando números racionales y el poder de las matemáticas y sus aplicaciones en la vida real.
¿Para qué sirven los números racionales? Más allá de los usos clásicos
Existen muchos otros contextos en que los números racionales están presentes y no notamos sus aplicaciones matemáticas ¿No nos crees? Pon mucha atención a lo siguiente:
Tiempo y organización diaria
Siempre cuando hablamos de tiempo hablamos de fracciones y números racionales: 15 minutos son 1/4 de hora, 30 minutos son 1/2 hora. Estas palabras las usamos todos los días, pero no somos muy conscientes del profundo componente matemático que poseen.
Un viaje en metro o en micro por Santiago se puede demorar 3/4 de hora; una película puede durar 1 hora y media; todo este lenguaje es muy habitual, pero pasa desapercibido por nuestra consciencia.
Expresemos matemáticamente el primer postulado centrándonos en las operaciones de los números racionales: Un viaje de 3/4 hora por Santiago.
1 hora dura 60 minutos, ¿Cómo determinamos cuánto son 3/4 de hora? Lo que tenemos que hacer es usar operaciones de números racionales, en este caso la multiplicación. Tenemos que multiplicar 3/4 x 60/1 de la siguiente forma:
(3/4) × 60 = (3 × 60) / 4 = 180 / 4, simplificando nos quedaría 45 minutos.
Tecnología y estadísticas
La matemática y la informática tienen una relación muy estrecha. Todos los días nos vemos enfrentados a datos y números relacionados con medidas de información digital, las que están directamente relacionadas a los números racionales y a fracciones.
Imagina que tienes un pendrive de 64GB y le metes información que pesa 48,5 GB. Te van a quedar 15,5 GB libres. Este número final es un número racional que también se puede expresar como fracción de la siguiente forma: 31/2. Además, algunos profesores matemáticas resaltan la importancia de aplicar estas conversiones en tecnología.
Ahora, si tienes, por ejemplo, 8GB de datos de internet y has utilizado 1,5 GB, ¿Cómo sabes cuánto has ocupado de tu capacidad total en términos de fracciones o números racionales?
Ocupemos algunas aplicaciones matemáticas de los números racionales y transformemos el número 1,5 a fracción. Esto queda: 3/2
Ahora ocupemos la división y dividimos 3/2 ÷ 8. Esto da como resultado 3/16. Entonces, has ocupado 3/16 partes del total.
¿Por qué es importante saber usar fracciones y decimales?
Ventajas de dominar este concepto en la educación y el trabajo
Como hemos visto las aplicaciones de los números racionales son muchas y están presentes en diferentes situaciones prácticas y matemáticas. No son solo teoría. Hay que trabajar con ellos y entenderlos. Mientras más cálculos mentales hagamos de fracciones y de nada número, mejor será nuestro manejo y uso de estas cifras.
En el trabajo, y en diferentes instancias educacionales, debemos potenciar el pensamiento lógico y matemático. Nuestro cerebro funcionará con mucha más agilidad si lo sometemos a esta variada práctica numérica y de porcentaje. ¡Usa los números racionales!
Consejos para identificar y manejar números racionales día a día
Identificar los números racionales es sencillo: puedes encontrar estas cifras en forma de fracciones, porcentaje y decimales. Cuando te enfrentes a operaciones que contengan números racionales, trata de calcular mentalmente y llegar a una solución rápida sin tocar una calculadora.
De esta forma podrás calcular las medidas en una receta, los diferentes descuentos, cada número en un impuesto, incluso medidas en distintas manualidades que eventualmente tengas que hacer. No lo dudes y recure siempre a las operaciones de números racionales.
Síntesis del artículo
En este artículo descubrimos el gran protagonismo que tienen los números racionales y las matemáticas en nuestro día a día. Desde su uso en la cocina hasta su aplicación en la informática, las fracciones siempre están presentes y nos las podemos topar en cualquier momento.
También entendimos que la utilización mental constante de los números racionales y sus operaciones (multiplicación, adición y sustracción de números racionales, además de división ) nos permitirán mejorar nuestra capacidad de resolver problemas y harán de nuestro cerebro un órgano más ágil y vivo.
Las aplicaciones matemáticas, en la teoría y en la vida cotidiana, de los números racionales nos permite tener un método para resolver situaciones complejas y obtener la solución a diversos problemas.
Resumir con IA:















