Sí, lo sabemos, aprender a derivar funciones puede ser complicado al inicio, pero este es uno de los pasos ¡más importantes dentro del cálculo diferencial! Y es que, las reglas de derivación permiten simplificar este proceso, ofreciendo fórmulas claras que nos evitan regresar a la definición formal de los límites en cada ejercicio.
Gracias a ellas, podemos resolver problemas de manera rápida y comprender mejor cómo cambian las funciones en diferentes contextos. Así que, ¿qué tanto sabes de las derivaciones matemáticas?
Pensando en ello, en Superprof Chile hemos preparado esta guía completa donde encontrarás un resumen de reglas derivadas, explicado de forma sencilla y acompañado de ejemplos fáciles. Te mostraremos cómo aplicar cada regla en casos prácticos, desde funciones básicas hasta expresiones compuestas, además de consejos y más, para que aprendas cómo derivar una función con seguridad y confianza:
¿Qué son las reglas de derivación y por qué son útiles?
Las reglas de derivación son un conjunto de herramientas del cálculo que nos permiten derivar funciones de manera rápida y ordenada, sin necesidad de regresar a la definición formal del límite. Gracias a estas reglas, el proceso de derivación se convierte en un método práctico que facilita el aprendizaje y la resolución de ejercicios.
Aprende más con nuestra guía completa sobre los límites y las derivaciones ¡haciendo click aquí!
Importancia de las derivadas en el cálculo
La derivada es uno de los conceptos centrales del cálculo diferencial porque nos muestra cómo cambia una función respecto a una variable. A través de ella podemos determinar la pendiente de la recta tangente en un punto, estudiar intervalos de crecimiento o decrecimiento y comprender el comportamiento local y global de un fenómeno. Además, las derivadas son la base de herramientas más avanzadas como las integrales, las series y las ecuaciones diferenciales, lo que las convierte en un pilar de las matemáticas modernas.
Aplicaciones básicas de las derivadas en la vida real
El alcance de las derivadas va mucho más allá del aula. En física, permiten calcular la velocidad instantánea y la aceleración de un cuerpo en movimiento. En economía, son clave para resolver problemas de optimización, como encontrar los máximos beneficios o los mínimos costos. En biología y otras ciencias, ayudan a modelar fenómenos como el crecimiento de poblaciones o la propagación de enfermedades. Incluso en la tecnología, se usan en simulaciones, gráficos y algoritmos que requieren medir cambios de manera precisa y por supuesto, que cuentan con muchas aplicaciones más...
Por otro lado, ¿conoces los límites matemáticos? Descubre más de este concepto aquí.
Diferencia entre derivar y aplicar una fórmula directamente
Muchas veces los estudiantes confunden el acto de derivar con la simple aplicación mecánica de una fórmula. Derivar implica comprender el proceso, identificar qué regla corresponde a cada caso y aplicarla correctamente para transformar una función en su derivada.
En cambio, memorizar fórmulas sin entenderlas puede llevar a errores o confusiones. La verdadera utilidad está en dominar el procedimiento, porque así podemos resolver expresiones más complejas, verificar resultados y aplicar el cálculo diferencial con criterio propio en distintos contextos.
Reglas básicas de derivación que debes conocer
Derivada de una constante
Cuando derivamos un número fijo, como 5, 10 o -3, su derivada siempre es 0, porque un valor constante no cambia, y la derivada mide precisamente el cambio de la función.
Ejemplo:
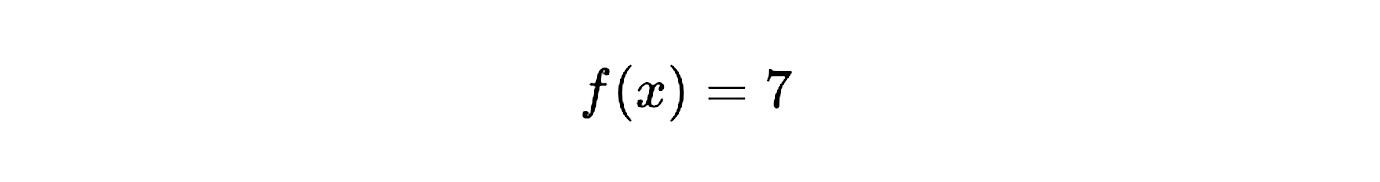
La derivada es:
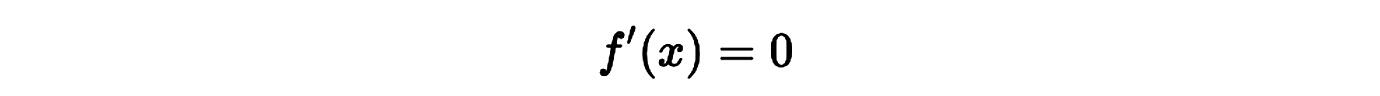
Otro ejemplo con una constante negativa:
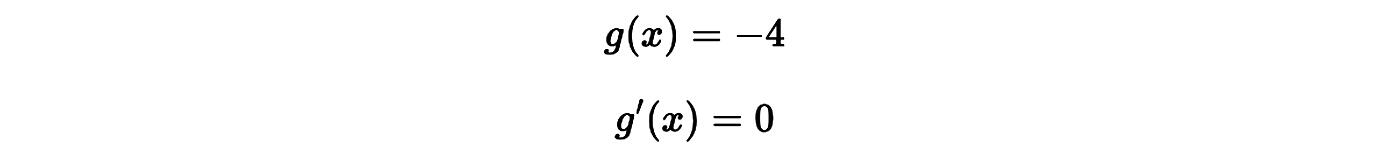
Idea clave: No importa el valor de la constante, su derivada siempre es cero. Esto simplifica mucho los cálculos cuando aparece un número fijo en una función.
Derivada de 𝑥
La variable 𝑥 respecto a sí misma tiene derivada 1, porque por cada unidad que aumentamos
𝑥, la función 𝑓(𝑥)=𝑥 también aumenta en 1 unidad.
Ejemplo:
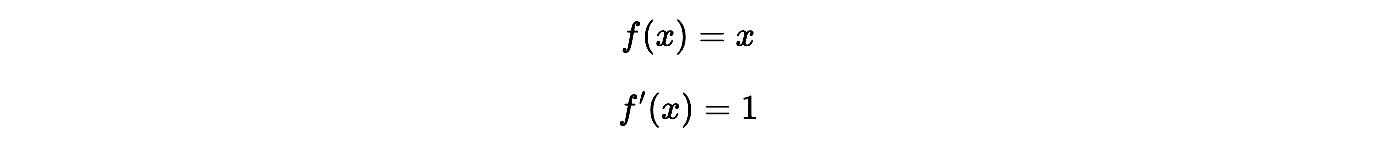
Si multiplicamos 𝑥 por un número:
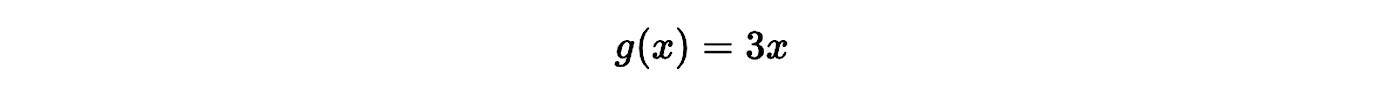
Aplicando la regla de la constante multiplicativa:
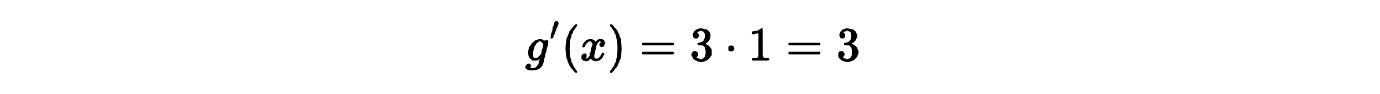
Idea clave: La derivada de 𝑥 es la base de muchas reglas, especialmente cuando trabajamos con funciones lineales.
Derivada de una función multiplicada por una constante
Si tienes una función 𝑓(𝑥) y la multiplicas por una constante 𝑘, la derivada se calcula multiplicando la constante por la derivada de la función.
Regla:
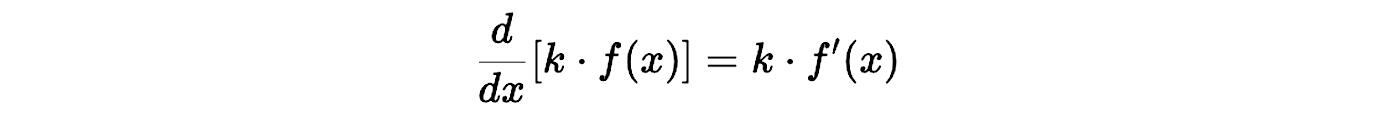
Ejemplo:
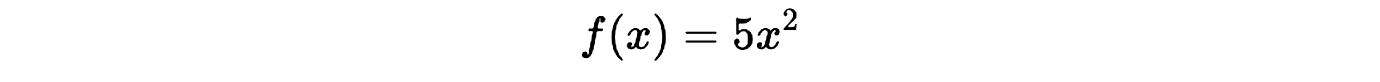
Primero derivamos x2 que es 2x, y luego multiplicamos por 5:
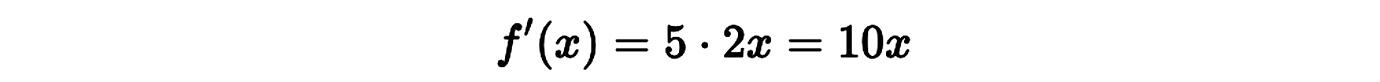
Otro ejemplo:
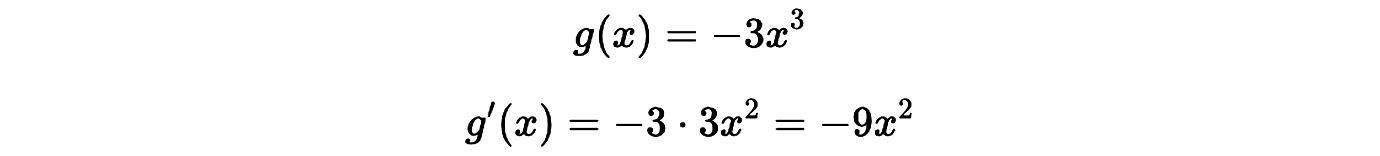
Idea clave: La constante no se deriva, solo se multiplica por la derivada de la función.
Derivada de una suma o resta de funciones
Cuando tenemos varias funciones sumadas o restadas, se deriva cada función por separado y se mantiene el signo correspondiente.
Regla:
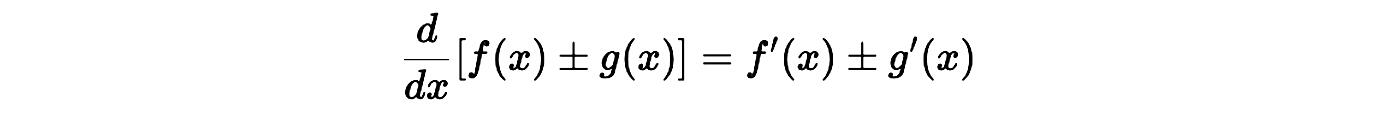
Ejemplo:
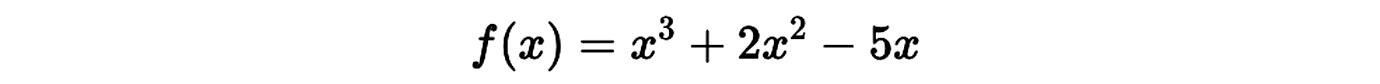
Derivamos término por término:
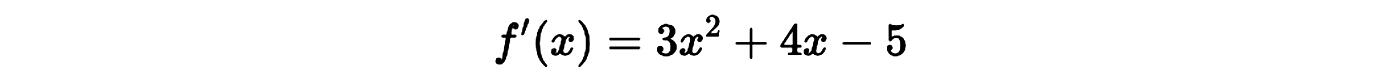
Otro ejemplo:
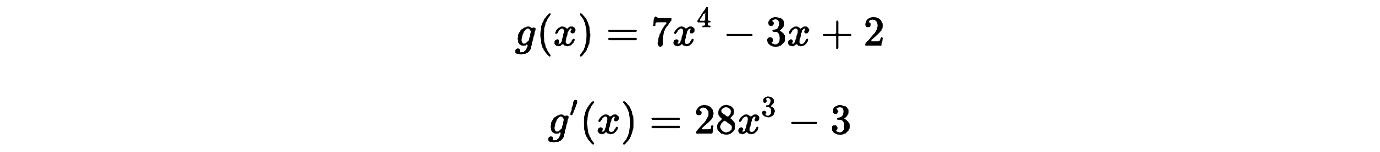
Idea clave: La derivación respeta la suma y la resta. Esto facilita derivar funciones largas sin perder precisión.
Reglas de derivación de funciones elementales
Derivadas elementales: potencias, raíces y funciones trigonométricas
Entre las derivadas elementales más comunes están:
- La de una potencia, que baja el exponente y resta 1.
- La de una raíz, que se puede expresar como potencia fraccionaria.
- Las funciones trigonométricas: la derivada de sen(x) es cos(x), mientras que la de cos(x) es −sin(𝑥).
Tabla rápida de derivadas comunes
Contar con una tabla resumida es clave para recordar reglas y avanzar más rápido en la práctica. Allí aparecen funciones polinómicas, exponenciales, logarítmicas y trigonométricas.
Ejemplos prácticos paso a paso
Ejemplo: si queremos derivar 𝑓(𝑥)= 3𝑥2+ 5𝑥, aplicamos la derivada fórmula de la potencia y obtenemos 𝑓’(𝑥)= 6𝑥 + 5. Este proceso se basa en reglas directas sin complicaciones.
Regla del producto y regla del cociente
Regla del producto: cómo se aplica y cuándo usarla
La regla del producto derivadas sirve cuando tenemos dos funciones multiplicadas. Consiste en derivar la primera y multiplicarla por la segunda, y luego hacer lo contrario.
Regla de la división: derivada de un cociente de funciones
La regla de la division derivadas se aplica cuando una función aparece en el numerador y otra en el denominador. Nos permite organizar la derivación sin caer en errores comunes.
Ejemplos de derivación usando ambas reglas
Por ejemplo, si tenemos un cociente con polinomios, podemos aplicar estas reglas para simplificar la expresión final y obtener la pendiente correspondiente.
También: Descubre cuáles son las propiedades de un límite matemático.
¿Qué son las reglas de derivación parcial?
Introducción al cálculo multivariable
Cuando pasamos al análisis de funciones de varias variables, aparece la necesidad de calcular derivadas parciales.
Derivadas parciales: cómo se diferencian de las derivadas comunes
A diferencia de una derivada ordinaria, las reglas de derivación parcial se aplican derivando respecto a una sola variable, mientras las demás permanecen constantes.
Ejemplo básico de derivada parcial de dos variables
Si 𝑓(𝑥,𝑦)=𝑥2𝑦+𝑦3, la derivada parcial respecto a 𝑥 es 2𝑥𝑦, mientras que respecto a 𝑦 es 𝑥2+3𝑦2.
Consejos para aprender a derivar con confianza
Identificar el tipo de función antes de derivar
Siempre debemos reconocer si trabajamos con polinomios, funciones trigonométricas, exponenciales o logarítmicas, ya que cada una tiene su regla específica.
Práctica con funciones reales y variadas
Cuanto más practiquemos con ejercicios que simulen casos reales, mejor entenderemos la notación y el proceso de derivación.
Recursos de apoyo: fórmulas y plantillas para recordar
Existen guías, resúmenes y recursos gratis que nos ayudan a recordar las reglas derivadas. También podemos usar una calculadora online, pero lo ideal es dominar el procedimiento manual.
Conclusión: dominar las reglas de derivación paso a paso
Las reglas básicas de derivación, junto con la regla del producto derivadas, la regla de la división derivadas y la regla de la cadena, son los pilares del cálculo diferencial.
¿Qué hacer después de aprender las reglas básicas?
Una vez dominadas, el siguiente paso es resolver ejercicios más complejos, aplicar las reglas derivadas en problemas reales y avanzar hacia derivadas parciales o implícitas.
Síntesis del artículo
En este artículo repasamos qué son las reglas de derivación, cómo aplicarlas en funciones simples y compuestas, y por qué son esenciales en el análisis matemático. Vimos ejemplos fáciles, tablas de apoyo y consejos prácticos para aprender cómo derivar una función paso a paso.
En Superprof Chile puedes reforzar estos conocimientos con la ayuda de un docente particular, practicar ejercicios personalizados y dominar la derivación con confianza. ¡Regístrate y empieza tu camino en el cálculo con un superprofe!
¿Te gustó este artículo? ¡Evalúalo!
Loading...
