El cálculo es una de las ramas más fascinantes de las matemáticas, y gran parte de su poder se debe al concepto de límite matemático. A través de él, los estudiantes pueden comprender el comportamiento de las funciones en distintos escenarios, desde un valor específico hasta cuando una variable tiende al infinito.
En Superprof Chile, muchos docentes especializados guían a los alumnos paso a paso en este proceso, utilizando ejemplos sencillos, teoría clara y ejercicios prácticos para fortalecer la confianza en el estudio de los límites matemáticos. Y una pequeña prueba de ello, es este artículo pensado en reforzar tus conocimientos sobre estos y claro, comprender más a fondo la aplicación de sus propiedades:
Pero antes, no te pierdas nuestra: Guía completa sobre la derivación y el límite.
¿Qué es un límite matemático y por qué es importante?
En matemáticas, un límite describe el valor al que se aproxima una función 𝑓(𝑥) cuando la variable independiente 𝑥 se acerca a un número específico. Se denota como:
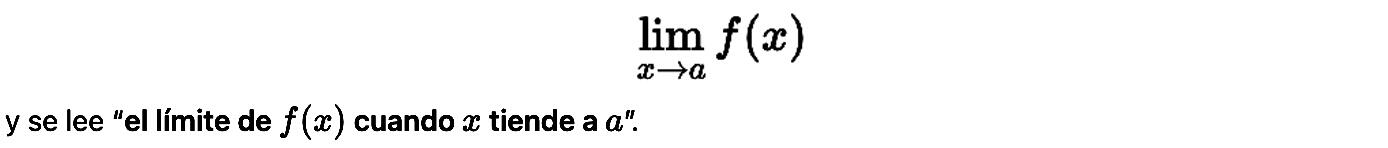
Esto significa que, aunque la función no siempre tome exactamente ese valor en 𝑎, sí se acerca progresivamente a él conforme 𝑥 se aproxima. Los límites son esenciales para definir la continuidad, calcular derivadas y comprender el comportamiento de una función en puntos críticos o cuando 𝑥 tiende al infinito.
Su rol en el estudio del comportamiento de las funciones
El límite matemático es clave para entender el comportamiento de las funciones en puntos donde la expresión no está definida o resulta difícil de evaluar. Gracias a los límites podemos predecir hacia dónde tiende una curva cuando la variable independiente se aproxima a cierto valor, incluso si en ese punto exacto la función no existe o presenta una discontinuidad.
Esto resulta fundamental para analizar conceptos como la continuidad de una función, la presencia de asíntotas verticales u horizontales, y los cambios bruscos en su comportamiento. En otras palabras, los límites nos permiten ver más allá de lo inmediato y comprender cómo se comporta una función en su entorno cercano, no solo en un punto aislado.
Aplicaciones en matemáticas y ciencias exactas
Los límites no solo son una herramienta teórica, sino que tienen aplicaciones prácticas en múltiples áreas:
⚡ Física: permiten calcular la velocidad instantánea de un objeto cuando el intervalo de tiempo tiende a cero.
💰 Economía: sirven para estimar la tasa de variación de costos, ingresos o beneficios en escenarios de optimización.
🏗️ Ingeniería: se utilizan para modelar procesos continuos, estudiar la estabilidad de sistemas y analizar el comportamiento de materiales bajo condiciones extremas.
En general, los límites constituyen la base para el desarrollo de derivadas e integrales en estas y muchas otras áreas. Pues, son pilares del cálculo diferencial e integral, siendo las herramientas esenciales para describir y predecir fenómenos en las ciencias exactas.
¿Quieres saber más de los límites? Hazlo aquí.
Principales propiedades de los límites
Antes de entrar a resolver ejercicios más complejos, es fundamental conocer las propiedades de los límites, ya que funcionan como “reglas” que simplifican el análisis de una función en un punto.
Estas propiedades nos permiten evaluar, simplificar y manipular expresiones sin perder rigor matemático, asegurando que los resultados cumplan con el cálculo y la lógica de las funciones reales. Así que, veámoslas a más detalle:
Límite de una constante
Cuando una función siempre devuelve un mismo valor (una constante), su límite será esa misma constante, sin importar a qué número tienda la variable.
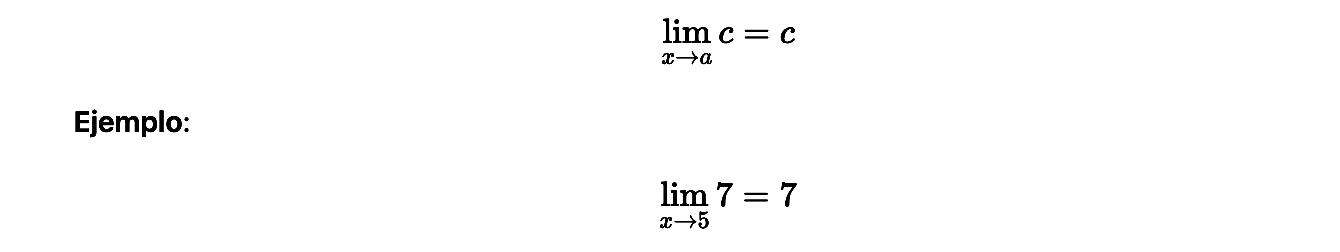
Aquí, sin importar el valor de 𝑥, la función vale siempre 7.
Límite de una variable
El límite de una variable independiente corresponde al número al que esta tiende.
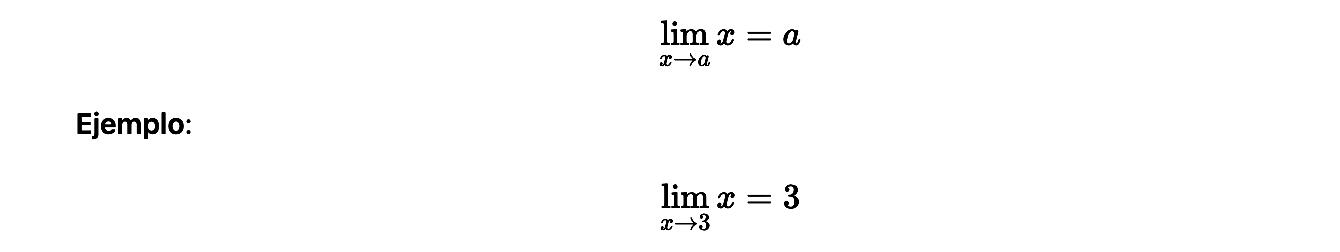
Esto refleja que la función “se acerca” directamente al mismo número que la variable.
Suma y resta de límites
El teorema de las operaciones establece que el límite de una suma o resta se obtiene sumando o restando los límites de cada función.
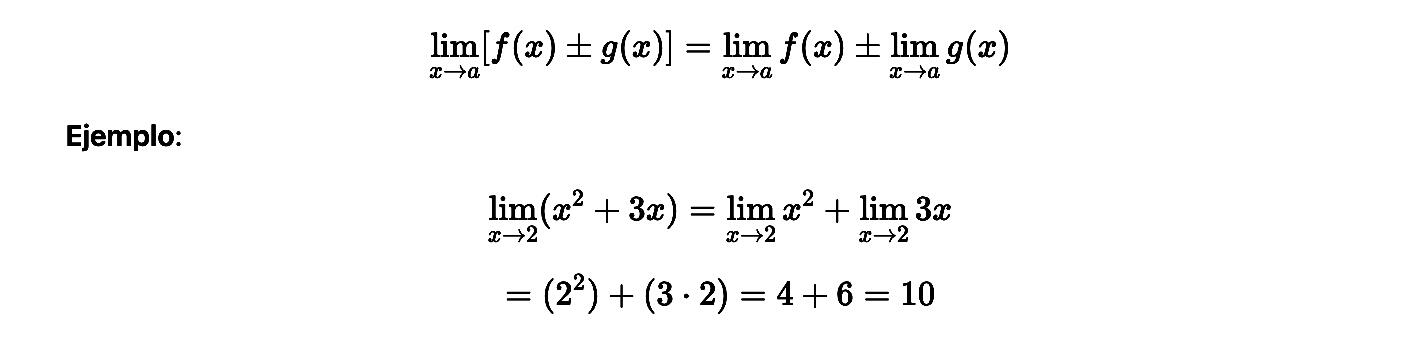
Producto y cociente de límites
De manera similar, el límite de un producto es el producto de los límites individuales:
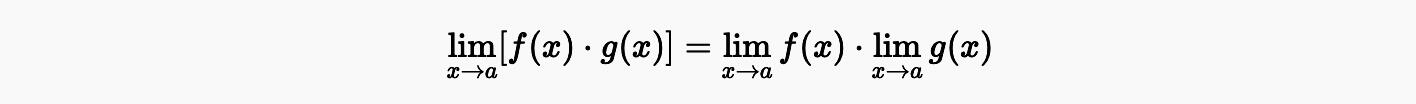
⚠️ En el cociente, el límite del denominador no debe ser cero:
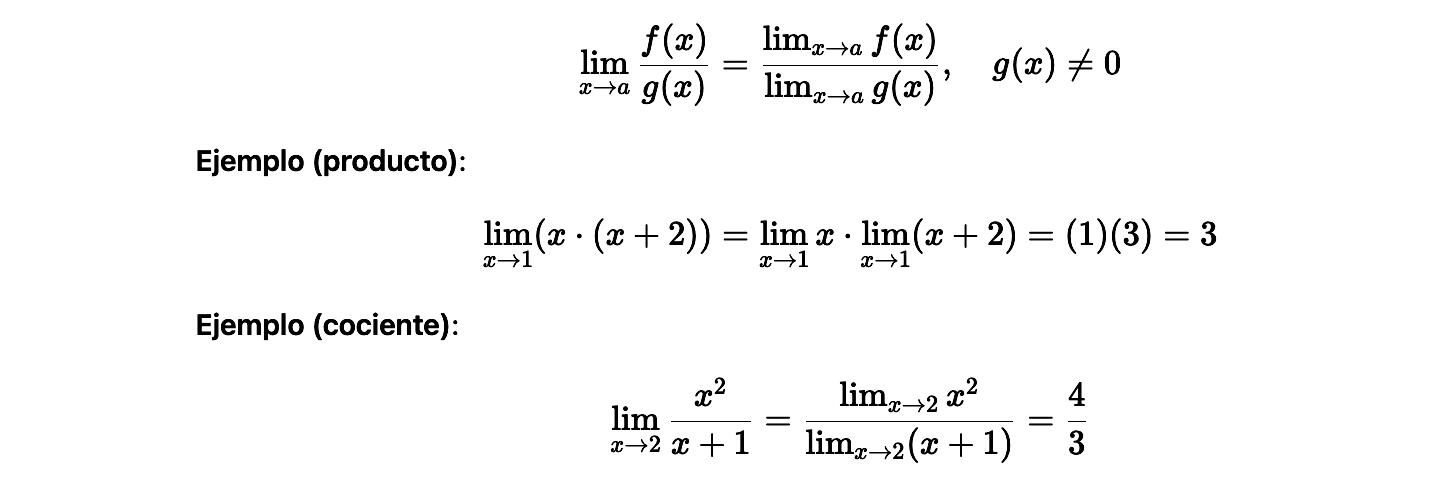
Límite de una función compuesta
Cuando una función está compuesta, el límite se conserva siempre que ambas funciones sean continuas en el punto de interés.
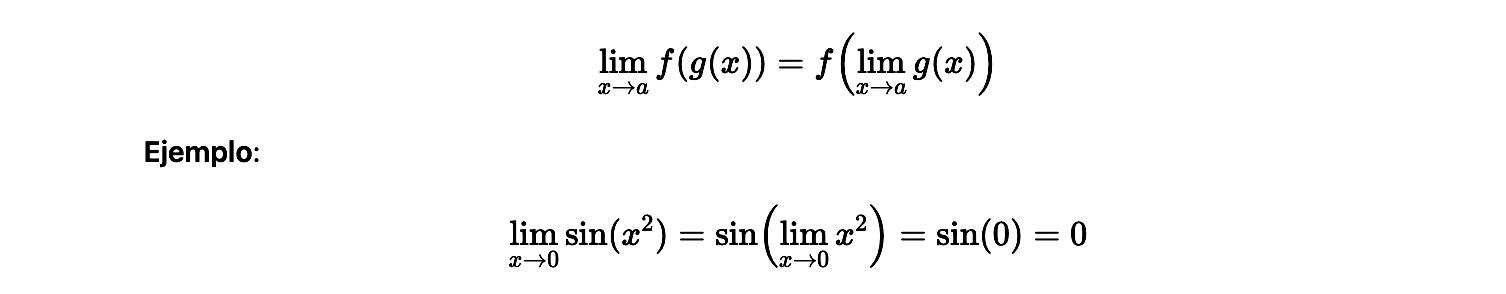
Propiedad del límite por factorización
Cuando el límite presenta una forma indeterminada como 0/0, podemos aplicar factorización para simplificar.
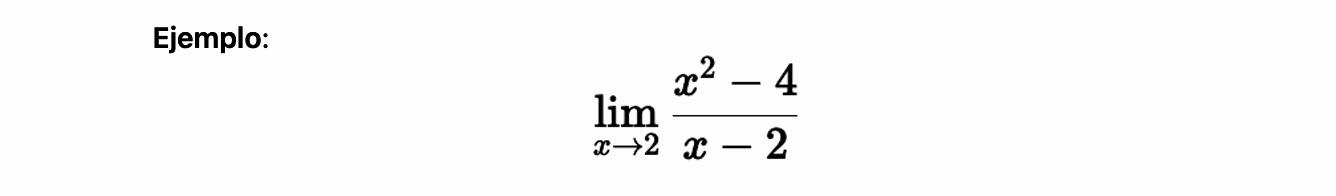
1. Factorizamos el numerador:
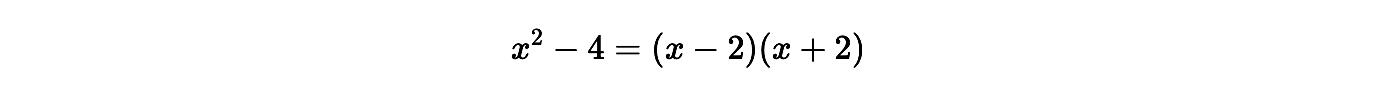
2. Simplificamos con el denominador:
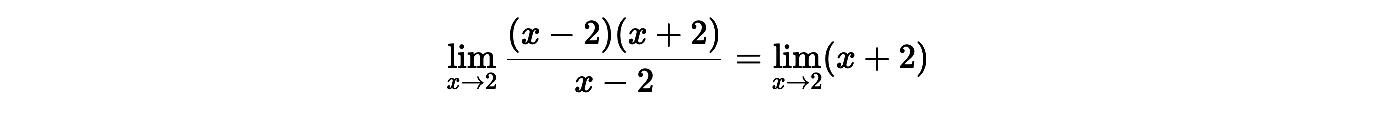
3. Evaluamos el límite:
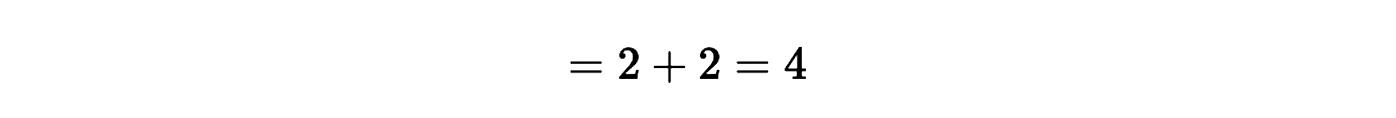
Como has podido ver, todas estas propiedades facilitan enormemente el trabajo con límites, ya que nos permiten simplificar, evaluar y hallar resultados de manera más directa, evitando cálculos innecesarios y resolviendo incluso casos donde aparecen indeterminaciones.
Ah, y por cierto, ¿qué tanto sabes de las derivaciones matemáticas?
¿Qué nos dicen estas propiedades sobre las funciones?
Las propiedades de los límites no son solo reglas algebraicas: representan herramientas clave para estudiar el comportamiento de las funciones en diferentes situaciones.
Gracias a ellas, podemos analizar cómo se comporta una función en puntos críticos, determinar su continuidad y comparar los distintos tipos de límites que aparecen en el cálculo.
Comportamiento en puntos críticos
Las propiedades límites nos permiten identificar qué ocurre cuando una variable se acerca a un punto donde la función puede dejar de ser suave, presentar un cambio abrupto o incluso una discontinuidad. Analizar estos puntos críticos ayuda a hallar intervalos donde la curva crece, decrece o tiende al infinito.
Análisis de continuidad y discontinuidad
Con el uso del límite matemático podemos evaluar si una función cumple con la condición de continuidad en su dominio. Si el límite existe y coincide con el valor de la función en ese punto, hablamos de continuidad. En cambio, si tiende a valores distintos por la izquierda (left) y la derecha (right), surge una discontinuidad o incluso una asíntota.
Comparación entre distintos tipos de límites
Estudiar los diferentes tipos de límites (finitos, infinitos, laterales, indeterminados) permite comprender el mismo fenómeno desde perspectivas distintas. Por ejemplo, el límite lateral nos muestra qué ocurre cuando nos acercamos a un valor por un solo lado del intervalo, mientras que un límite infinito revela tendencias de crecimiento sin acotación. Esto facilita el cálculo de trayectorias, la evaluación de funciones racionales y la identificación de comportamientos potenciales en matemáticas y ciencias exactas.
Y como ya aprendiste esto, ahora: Aprende cuáles son las reglas básicas de una derivación ¡aquí!
Tipos de límites en matemáticas
Los límites matemáticos se presentan en distintas formas según el comportamiento de la función y el punto que analizamos en su dominio. Conocerlos es esencial para el cálculo y el estudio de las funciones reales:
Límite finito en un punto
Se da cuando una función tiende a un valor numérico exacto a medida que la variable se acerca a un número específico. Este caso refleja continuidad local y permite evaluar el comportamiento sin saltos ni rupturas.
Límite infinito
Ocurre cuando la función crece sin límite, ya sea hacia +infinito o –infinito, al acercarse a cierto valor del intervalo. Estos escenarios se asocian con la presencia de asíntotas verticales en la gráfica de la función.
Límite lateral (derecho e izquierdo)
Se distingue entre el límite por la izquierda (left) y por la derecha (right) cuando la variable se aproxima a un mismo punto desde lados distintos. Analizar ambos nos permite determinar continuidad o identificar discontinuidades.
Límites indeterminados y su interpretación
Expresiones como 0/0 o ∞/∞ no tienen valor definido de forma directa y se consideran indeterminaciones. Para resolverlas, se aplican leyes del cálculo, factorización de numerador y denominador, simplificación con raíz, potencia o el uso de funciones trigonométricas como sen y cos.
Errores comunes al trabajar con propiedades de límites
❌ Mal uso de las operaciones con límites
Aplicar reglas de suma, resta o cociente sin verificar si el denominador es cero.
❌ Confusión entre límite y valor de la función
El valor del límite no siempre coincide con la función en ese punto, especialmente en funciones no continuas.
❌ No considerar la existencia del límite antes de aplicar propiedades
No todos los límites existen. Es necesario evaluar antes de usar las propiedades.
¿Cómo se relacionan los límites con las propiedades de funciones?
Los límites son una herramienta esencial para comprender las propiedades de funciones, ya que nos muestran cómo se comporta una función en un punto específico y también cuál es su tendencia general en un intervalo.
Y como ya habrás notado, estos son fundamentales para estudiar crecimiento, decrecimiento, máximos y mínimos, aportando una visión completa del comportamiento de las funciones tanto a nivel local como global.
Comportamiento local y global
🔎 El límite matemático describe el comportamiento local de una función en un punto.
Cómo los límites permiten detectar tendencias y cambios bruscos
📈 Permite detectar tendencias, saltos o cambios bruscos en la gráfica.
Su uso en el análisis de crecimiento y decrecimiento
📊 Es clave para identificar intervalos de crecimiento, decrecimiento, máximos y mínimos.
Conclusión
¿Por qué los límites son la base del cálculo moderno?
Los límites son la herramienta fundamental del cálculo, sin ellos no existiría la derivación ni la integración.
Consejos finales para estudiar propiedades de límites con claridad
Repasar la definición, practicar con muchos ejemplos y apoyarse en recursos como apuntes en PDF o lecciones con un tutor especializado, ayuda a entender mejor los tipos de límites y las propiedades de funciones.
Síntesis del artículo
Las propiedades de los límites permiten analizar el comportamiento de las funciones y entender fenómenos que aparecen en distintas disciplinas. Desde el límite de una constante hasta casos más complejos como los límites indeterminados, todos ellos son esenciales para estudiar continuidad, tendencias y crecimiento.
¡Confía en nosotros! Ya verás que con la práctica constante y el apoyo de Superprof Chile, cualquier estudiante puede dominar el uso de límites y avanzar con seguridad en el cálculo.
¿Te gustó este artículo? ¡Evalúalo!
Loading...
