«Todo número iluminado tiene su sombra dorada» - Nabil Alami
El número áureo, también llamado razón dorada, proporción áurea o proporción divina, es una proporción definida como el valor numérico de la proporción que guardan entre sí dos segmentos de recta a y b (a más largo que b). La longitud total, suma de los dos segmentos a y b, es al segmento mayor a, lo que este segmento a es al menor b: (a + b)/a = a/b.
También es designado por la letra griega φ (phi). Es un número irracional, única solución de la ecuación x2 = x + 1. Su valor es alrededor de 1,6180339887.
Una infinidad de alumnos toman clases particulares, muchos de ellos de matemáticas. Aunque se suele considerar una asignatura difícil, las Matemáticas pueden ser divertidas y contener misterios fascinantes. Vamos a hablar de uno de ellos: el número áureo.
Descubre con Superprof los números más famosos de las Matemáticas.

El número áureo: orígen

Para conocer el origen de la proporción áurea necesitamos remontarnos hasta el siglo XVI. Leonardo Pisano, también conocido como Fibonacci, fue un famoso matemático italiano, que contribuyó a divulgar por Europa el sistema de numeración árabe con base decimal que seguimos usando a día de hoy.
El gran descubrimiento de este matemático fue la sucesión de Fibonacci, que dio lugar más tarde a la proporción áurea. Esta proporción pasaría a relacionarse con la belleza o la naturaleza, y a utilizarse en arte y pintura por generaciones.
El primer texto matemático que hace referencia al número áureo fue escrito por Euclides (300 a.C.), que lo define de la siguiente manera: «Se dice que una recta ha sido cortada en extrema y media razón cuando la recta entera es al segmento mayor como el segmento mayor es al segmento menor».
En el Renacimiento, al número áureo se le llama divina proporción y se le atribuye una intervención divina según el libro de Pacioli, ilustrado por el famoso Leonardo da Vinci.
Fue también en esta época cuando la sucesión de Fibonacci se relaciona con el número áureo. Al dividir un término de la sucesión por su término anterior, el resultado se acerca al número áureo. La aproximación es mayor cuando el término es alto.
Lee también nuestro artículo sobre los números perfectos.
Números áureos ¿Qué es la sucesión de Fibonacci?
Cuando hablamos de la sucesión de Fibonacci hablamos de una sucesión numérica infinita.
Es la siguiente: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, etc.
En la sucesión de Fibonacci la suma de dos números consecutivos siempre da como resultado el siguiente número. Además, la relación que existe entre cada pareja de números, se va aproximando cada vez más a un número en concreto: el número áureo. Es decir, si dividimos cada número de la secuencia con su número anterior, el resultado obtenido se va aproximando cada vez más al valor del número áureo y la diferencia es cada vez menor a medida que tomamos valores mayores en la sucesión.
¿Buscas un clases de matematicas online? ¡En Superprof podemos ayudarte a encontrar lo que necesitas!

El número áureo en geometría
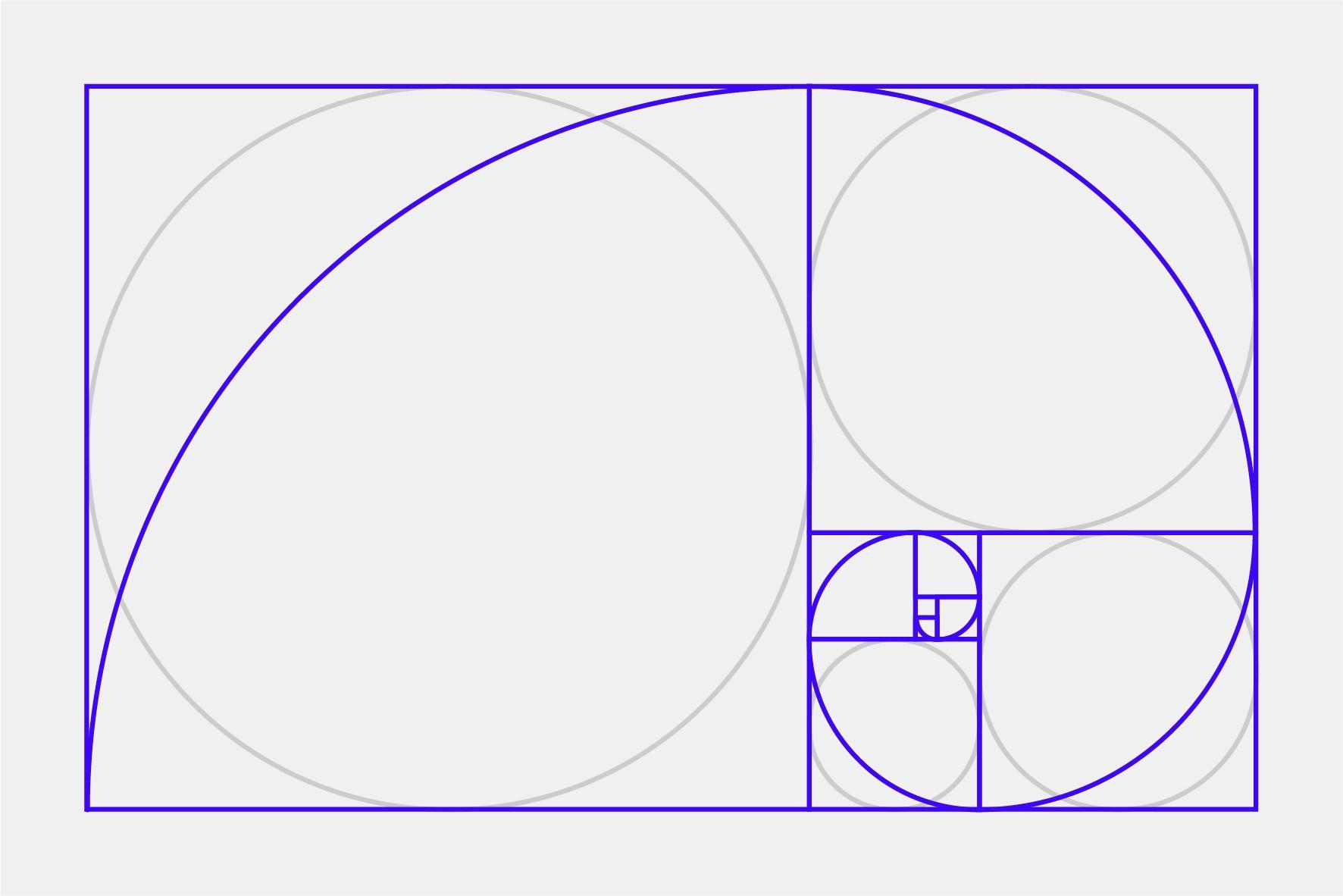
La primera definición de la proporción áurea es geométrica. El teorema es el siguiente: «Dos longitudes a y b (estrictamente positivas) respetan la proporción áurea si la relación de a sobre b es igual a la relación de a + b sobre a».
A la luz de los trabajos de Euclides, surge una nueva definición de la proporción áurea:
«El número áureo es el número real positivo, denotado por φ, igual a la fracción a/b si a y b son dos números en proporción de extrema y media razón».
¡En Superprof puedes encontrar clases particulares de matematicas!
Esta es la fórmula correspondiente: φ = (1 + √5) / 2.
φ es la solución de una ecuación de segundo grado, que da una tercera definición: «El número áureo es la única solución de la ecuación x2 - x - 1 = 0».
Gracias a estos cálculos, es posible dibujar una proporción de extrema y media razón usando un compás, una regla y una escuadra:
- Dibuja un círculo C de radio 1,
- Al final del radio 1, dibuja un segmento de longitud 1/2, perpendicular al radio,
- Dibuja el círculo C’ de radio 1/2 colocando la punta del compás al final del segmento de longitud 1/2 previamente dibujado,
- Dibuja el segmento desde el centro del círculo C hasta el final del círculo C’, pasando por el centro del círculo C’,
- La longitud de este segmento tiene el valor del número áureo.
A partir de estos círculos, puedes construir un rectángulo áureo.
También podemos integrar un cuadrado de lado a - b en el rectángulo áureo de lados b × (a - b). Al añadir un cuarto de círculo en cada cuadrado, obtenemos una espiral, llamada espiral dorada.
Descubre nuestra oferta de clases de matematicas en Superprof.
El número áureo en aritmética

El otro método para definir el número áureo es algebraico. En álgebra, el número áureo se define como la única raíz positiva de una ecuación.
Usando ambos enfoques, algebraico y geométrico, es posible resolver una ecuación de segundo grado. Esto se llama álgebra geométrica. φ 2 = 1 + φ tiene por solución el número áureo.
La proporción dorada también se puede alcanzar usando la fracción continua en el infinito: 1 + (1/(1 + (1/1))).
Por cierto, ¿ya lo sabes todo sobre el número Pi?
Relación aurea: ejemplos
Como puedes ver, el número áureo está omnipresente en las Matemáticas, pero también a nuestro alrededor. En la naturaleza, la proporción dorada está presente a través de varios elementos:
- Las escamas de una piña de pino generan espirales logarítmicas que pueden producir la sucesión de Fibonacci;
- Los estambres de un girasol responden al mismo fenómeno;
- Los cristales de cuarzo se forman en un patrón pentagonal, en el que interviene el número áureo;
- La corteza de una piña induce una espiral ordenada asociada con la proporción áurea.
Pero la filotaxis del girasol y la cristalografía de cuarzo no siempre siguen las reglas de la proporción áurea, por lo que es difícil ver un fenómeno místico o divino. Tal vez sea solo una coincidencia...
Echa un ojo también a nuestro artículo sobre el número i.

La cuestión de si el cuerpo humano está vinculado o no a la proporción áurea se ha planteado repetidamente, ya sea de naturaleza científica, artística o estética.
Zeising intentó medir el cuerpo humano utilizando solo el número áureo, pero lo descartó rápidamente. Las proporciones del cuerpo humano así dibujadas no eran realistas. Además, las dimensiones del cuerpo humano cambian constantemente. Los seres humanos crecen a medida que evolucionan y no necesariamente de manera uniforme.
Sin embargo, la búsqueda de la proporción dorada en el cuerpo humano no se ha abandonado. Hoy en día, los científicos se centran en el cerebro para descubrir un vínculo con la proporción áurea, pero esta teoría sigue siendo controvertida.
¿Quieres saber más sobre el número e? Toma nuestras clases particulares de matemáticas.
La proporción dorada no solo fascina a los científicos, sino que está presente en muchos ámbitos como la pintura, especialmente la del Renacimiento. Recuerda que en ese momento al número áureo se le llamaba divina proporción. Lo encontramos en el cuadro de El nacimiento de Venus de Botticelli.
Pero a veces, son interpretaciones tardías y no hay voluntad por parte del artista como lo sugiere el cuadro de San Jerónimo de Leonardo da Vinci en el que encontramos el rectángulo áureo.
El uso de la proporción áurea en muchos edificios antiguos es un tema de controversia. Es difícil saber si los constructores eran conscientes del uso de la proporción áurea o si es una sobre interpretación de los arqueólogos.
Hay varios ejemplos:
- El teatrode Epidauro.
- La gran pirámide de Giza.
- La fachada del Partenón según las convenciones.
- Una antigua torre en Modon.
- El gran altar de Pérgamo.
- Una lápida funeraria de Edesa.
- Una tumba en Pella.
¿Te interesa conocer también el número 0?
Por otro lado, más recientemente, el arquitecto Le Corbusier teoriza el uso de la proporción áurea y crea un sistema llamado Modulor que utiliza en muchas de sus construcciones como la Ciudad radiante de Marsella o la Capilla de Notre-Dame-du-Haut de Ronchamp.
También en la música, el número áureo se busca en la armonía y el ritmo. La aproximación más cercana al número áureo es la sexta menor obtenida por dos sonidos cuya frecuencia define una relación de 8/5 = 1,6.
Pero ¿Cómo saber mi número áureo? Si dividimos el lado del cuadrado (la altura del ser humano) por el radio de la circunferencia (la distancia del ombligo a la punta de los dedos) tendremos el número áureo.
Y podríamos continuar la lista, ya que la presencia del número áureo fascina enormemente y es el tema de teorías más o menos científicas y verificadas.
Resumir con IA:















