Las ecuaciones diofánticas (también conocidas como diofantina), nombradas así por Diofanto de Alejandría, matemático de la antigua Grecia, son ecuaciones algebraicas de dos o más incógnitas.
La solución que buscan encontrar este tipo de ecuaciones son en números enteros, no en números reales.
¿Qué quiere decir esto?
Significa que la solución de estas ecuaciones, donde hay 1 o 2 incógnitas, tiene que ser:
- Número natural
- Sus inversos negativos
- O el cero
Esta la forma de una ecuación diofántica:
- ax+by=c
En esta ecuación a, b y c son números enteros.
Entonces, “x” e “y” son las variables que se busca encontrar.
Descubre a continuación el misterior de los números primos.

Graficándolas un poco más, podríamos expresar esta ecuación de la siguiente forma:
- 3x+5y=7
Una ecuación diofántica también es una ecuación polinómica.
Esto sólo significa que las variantes tienen la posibilidad de ser elevadas a potencias enteras positivas.
También se pueden multiplicar entre si y este resultado formará también términos polinómicos.
Ecuaciones y Pitagoras
Las ecuaciones pitagóricas son ecuaciones que se expresan de la siguiente forma:
- X2 + y2= z2
Donde x, y, z son números enteros.
La terna pitagórica es cualquier terna, y con esto nos referimos a X, Y, Z, que solucione esta ecuación.

¿Cuántas soluciones tiene una ecuación Diofántica?
Para responder esta pregunta, primero revisemos un ejemplo de una ecuación diofántica:
- X + Y = 5
Si el resultado de esta ecuación fuese en números reales, el problema tendría múltiples resultados.
Pero recuerda que los resultados de las ecuaciones diofánticas son sólo en número enteros.
Al encontrar las soluciones de esta ecuación diofántica en números enteros sólo tendremos cuatro (4) resultados.
Estos son:
X e Y pueden ser las siguientes cifras correspondientemente:
- (1, 4)
- (2, 3)
- (3, 2)
- (4, 1)
Ecuación cuadrática formula y resoluciones
¿Qué sabemos de las ecuaciones cuadráticas?
Bueno, estas ecuaciones son:
- Polinómicas
- De segundo grado
Descubre qué son y para qué sirven los números trascendentes.
Además, las ecuaciones cuadráticas se pueden expresar de la siguiente forma:
- ax2+bx+c=0
En esta ecuación “a” tiene que ser diferente a cero (“0”)
Y la letra “x” es la variable.
En cambio, a, b, c son constantes.
Ahora para encontrar la solución de esta ecuación hay que utilizar la siguiente fórmula:
- x=-b±√b²-4ac / 2a
Resolvamos la siguiente ecuación cuadrática utilizando su fórmula:
- 2x2−4x−6=0
Lo primero que tenemos que hacer es identificar los valores en la fórmula y reemplazarlos.
- a = 2
- b = −4
- c = −6
Entonces quedaría:
- x=-4(-4)±√-(-4)²-4 x 2 x (-6) / 2 x 2
- x=-4(-4)±√64 / 2 x 2
Esto sería igual a:
- x= 4 ± 8/ 4
Como tiene dos símbolos opuestos (postivo y negativo), la ecuación puede tener dos posibilidades de resolución.
Estas son:
- x=4 + 8 / 4 = 3
- x=4 - 8 / 4 = 1
Resultados:
- X= 3
- X= 1


¿Cómo saber si una ecuación Diofántica tiene solucion?
No existe un método único y preciso para determinar si una ecuación diofántica tiene solución.
Los criterios de solución son varios.
Estos métodos pueden usarse sólo para ciertos tipos de ecuaciones diofánticas.
Conoce qué son los enigmaticos números perfectos.
Solución en ecuaciones lineales
Revisemos la solución para esas ecuaciones que no ofrecen mayor complicación, que son las más simples: las ecuaciones lineales.
Ejemplo: ax + by= c
Esta ecuación podría tener una solución, pero para que exista tal, se debe cumplir que:
El número mayor que divide a los coeficientes “a” y “b” también divide a “c”.
A esta cifra se le conoce como Máximo común divisor o MCD.
Soluciones en ecuaciones Cuadráticas Diofánticas
La solución de estas ecuación ofrece un poco más de complejidad.
Pongamos el ejemplo de la siguiente ecuación cuadrática:
- x2 + y2= z2
En este tiple pitagórico existe soluciones, pero:
Estas soluciones se generan usando dos números enteros m y n.
Además, x, y , z se obtienen mediante ciertas fórmulas que dependen de m y n.
¿Quién creó las ecuaciones diofánticas?

Encontramos rastros de la presencia de las ecuaciones diofánticas desde la antigua Grecia.
En el siglo III antes de Cristo existió Diofanto de Alejandría.
Para comprender mejor estos conceptos y su aplicación en la matemática, un profesor matemática puede orientarte en el estudio de este fascinante campo.
Este matemático helénico es el padre de este tipo de cálculo.
En su escrito "Arithmetica" se aprecian ya las bases para entender mejor las ecuaciones diofánticas.
En esta obra, Diofanto nos entrega un enfoque práctico sobre la resolución de este tipo de ecuaciones.
Además, utilizó técnicas didácticas, las que aplicó en la resolución de problemas matemático presentes en la vida cotidiana.
Más contribuciones
Mucho más adelante, distintos matemáticos, todos en su respectiva época, también constribuyen al avance y entendimiento de este de las ecuaciones diofánticas.

En el siglo XVII, Pierre de Fermat, aseguró que “no existen soluciones enteras positivas para este tipo de ecuaciones”
UN siglo más adelante, en el siglo XVIII, Leonhard Euler contribuyó ocupando métodos diferentes y adicionales para resolver las ecuaciones diofánticas.
Ecuaciones que antes eran impenetrables, Euler las resolvió y expuso para que las matemáticas puedan seguir avanzando.
Por su parte, Carl Friedrich Gauss, en el siglo XIX, realizó su obra "Disquisitiones Arithmeticae", ayudando a desarrollar la teoría de números.
Gauss aportó con el concepto de Congruencias y encontró soluciones enteras para ecuaciones polinómicas, ayudando a que las matemáticas puedan entrar en la teoría moderna de números.
¿Quieres aprender estadística? ¡Toma una clase estadistica con Superprof!
En la actualidad
Hoy en día, las ecuaciones diofánticas son la base de algunos algoritmos.
En los sistemas de criptografía de claves RSA las ecuaciones diofánticas intervienen como problemas para resolver.
También estas ecuaciones están presentes en la informática, sobre todo en lo que gira en torno a la teoría de la complejidad.
Cuando se trata de grandes conjuntos de datos, estas ecuaciones también contribuyen, sobre todo a la hora de optimizar el diseño de algoritmos.
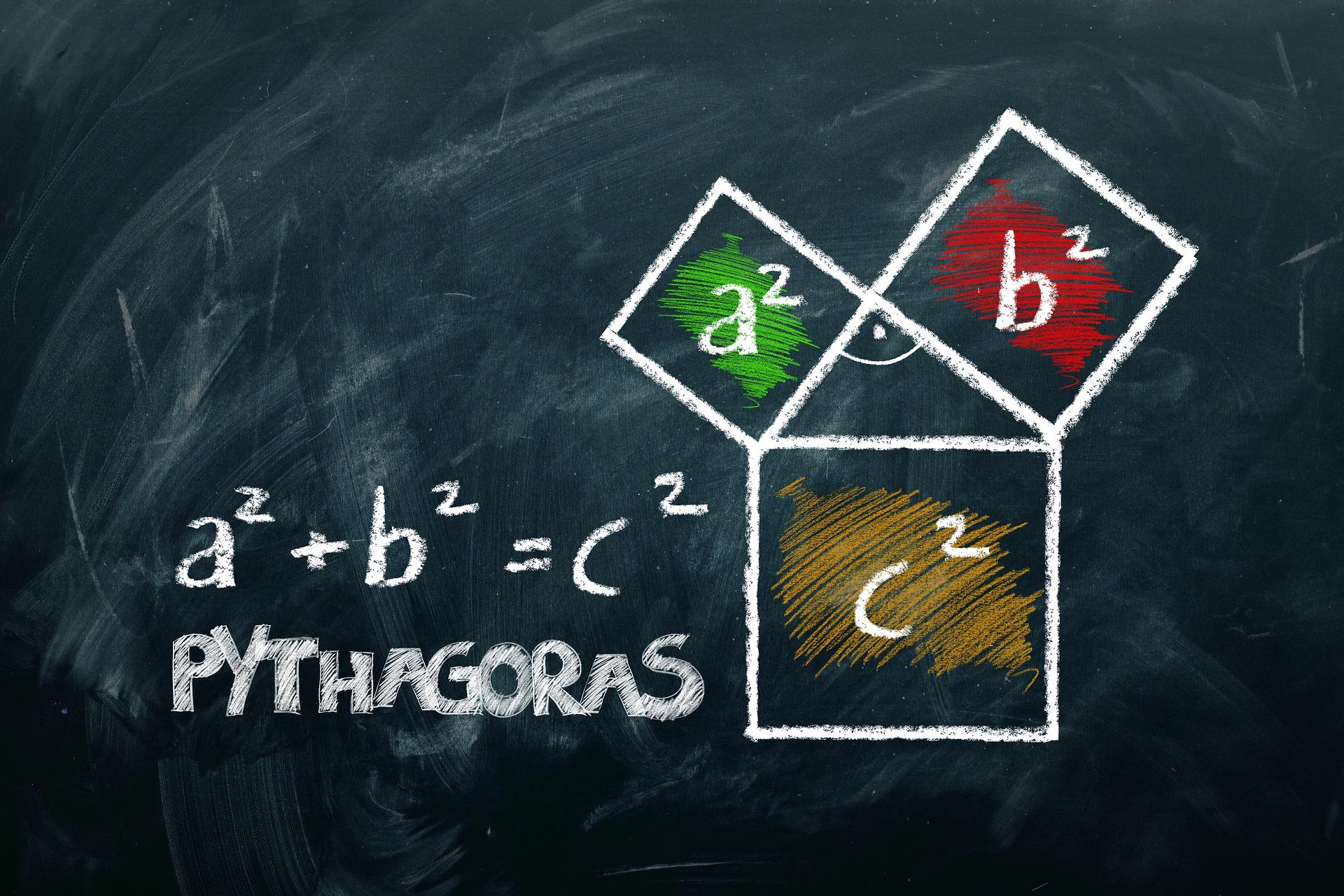
En la actualidad, la ciencia y la tecnología acuden a la matemática para poder formular mecanismos que les permitan funcionar con efectividad y automatización.
En esto las ecuaciones diofánticas tienen mucho que decir.
Conoce y sorprendete con las funciones aritméticas.
¿Qué significa ecuación Diofántica cúbica?
Una ecuación diofántica cúbica no es más que una ecuación polinómica, pero de tercer grado.
Esto quiere decir que las variables están elevadas al cubo, o sea, al exponen tres (3)
Pero ¿qué significa que una ecuación Diofántica tenga diferentes grados?
Recapitulando, podemos decir que cada ecuación diofántica puede ser clasificada por estos grados.
Podemos encontrar ecuaciones diofánticas:
- Lineales (Grado 1)
- Cuadráticas (Grado 2)
- Cúbicas (Grado 3)
Incluso podemos encontrar algunas de mayor grado.
Un dato curioso es que este tipo de ecuaciones están muy vinculadas a la teoría de números.
Para resolver una ecuación diofántica se pueden usar herramientas y conceptos relacionados con algunas teorías de números.
Por ejemplo:
- El teorema fundamental de la aritmética
- El teorema chino del resto
- La conjetura de Goldbach
Las preguntas sobre las ecuaciones diofánticas aún son muchas.
Durante siglos y siglos, matemáticos de todas partes del mundo han aportado con sus conocimientos y conclusiones al entendimiento de estas ecuaciones
Sin embargo, aún hay cuestiones pendientes…
Hoy por hoy, el interés por tratar de explicar en su totalidad las ecuaciones diofánticas continúa vigente.
Técnicas y métodos se ponen en la mesa, y cada día se avanza más y más hacia la siguiente estación de la matemática contemporánea.
Resumir con IA:















