Aprender a trabajar con derivadas es uno de los retos más importantes dentro del cálculo diferencial. Este concepto permite analizar la tasa de cambio de una función, interpretar la pendiente de una curva y explicar fenómenos dinámicos en matemáticas y ciencias aplicadas.
Es por eso que en Superprof Chile hemos preparado esta guía en la que descubrirás qué son las derivadas, cómo se calculan paso a paso, cuáles son sus aplicaciones más relevantes y qué tipos de derivadas debes conocer para avanzar en tu estudio del análisis matemático.
Todo ello y más, con ejemplos claros, ejercicios prácticos y consejos útiles que podrás dominar con constancia o junto a un superprofe especializado en cálculo:
Pero antes, descubre más en nuestra guía completa sobre límites y derivaciones ¡aquí!
Introducción a las derivadas
Hablar de derivadas es entrar al corazón del cálculo diferencial, una de las ramas más influyentes de las matemáticas modernas. Pero antes de entrar en fórmulas, conviene entender qué es una derivada en términos simples: se trata de una herramienta que nos permite medir cómo cambia una función respecto a su variable.
¿Qué es una derivada en términos simples?
Cuando una recta tangente toca una curva, la pendiente de esa tangente indica la tasa de cambio de la función en ese punto. Esa pendiente es la derivada. En otras palabras, responde a la pregunta: ¿qué tan rápido cambia una función en un instante determinado?
Breve historia y contexto del cálculo diferencial
El cálculo diferencial tiene sus raíces en el siglo XVII, cuando dos grandes matemáticos, Isaac Newton en Inglaterra y Gottfried Wilhelm Leibniz en Alemania, formularon de manera independiente los fundamentos de la derivación. Newton utilizó las derivadas para modelar el movimiento de los cuerpos celestes y sentar las bases de la física clásica, mientras que Leibniz introdujo una notación clara y elegante que todavía utilizamos hoy, con símbolos como dy/dx o d/dx.
Fue que con estos personajes, el estudio de la pendiente de una recta tangente, la velocidad instantánea o la tasa de cambio ¡dejó de ser un problema abstracto! para convertirse en una herramienta universal. Desde entonces, el cálculo diferencial no solo revolucionó la física, sino también la economía, la ingeniería y muchas ramas de las ciencias exactas, consolidándose como un lenguaje fundamental para describir el cambio en la naturaleza y en los procesos humanos.
¿Por qué las derivadas son tan importantes?
Las derivadas son fundamentales porque nos permiten medir y describir el cambio con exactitud matemática. Gracias a ellas podemos calcular la velocidad instantánea de un automóvil, determinar cómo varía la temperatura en función del tiempo o analizar el crecimiento de una población.
En otras palabras, la derivada convierte situaciones dinámicas en expresiones numéricas claras, lo que hace posible predecir, optimizar y comprender fenómenos en la física, la biología, la economía o la ingeniería.
Por otro lado, ¿qué tanto sabes de los límites realmente?
Concepto formal de derivada
Definición matemática y notación habitual
Formalmente, la derivada de una función 𝑓(𝑥) en un punto 𝑎 se define como:
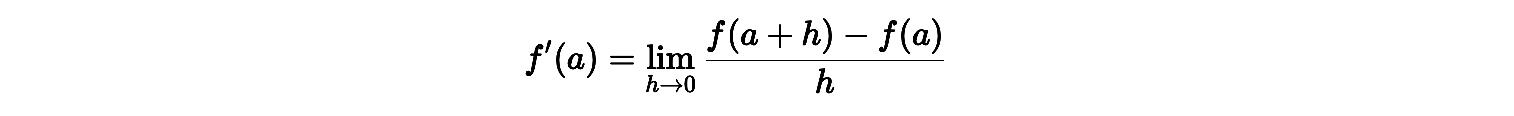
Esta definición usa la notación de Leibniz dy/dx y también la de Newton, representada con un punto sobre la variable.
Relación entre la derivada y la pendiente de una recta tangente
El límite anterior calcula la pendiente de la recta tangente en el punto de la curva. Si la función es continua y diferenciable en ese intervalo, la pendiente existe y podemos evaluarla con exactitud.
Interpretación gráfica y práctica
Visualmente, derivar es acercarse con dos puntos cada vez más próximos sobre la gráfica de una función y observar la pendiente que resulta cuando la distancia tiende a cero.
Conoce las propiedades matemáticas de un límite ¡aquí!
¿Cómo se calcula una derivada?
Para entender cómo se deriva, debemos aplicar la definición de límite y simplificar hasta hallar la solución.
Derivadas fundamentales: funciones más comunes
Las derivadas fundamentales son reglas rápidas que aplicamos sobre funciones conocidas:
- Derivada de una constante: Toda constante es “plana”, no cambia, por eso su derivada siempre es cero.
- Derivada de una potencia de 𝑥: Es la famosa regla de la potencia, probablemente la más usada en cálculo.
- Funciones trigonométricas básicas: Estas derivadas muestran la relación cíclica entre seno y coseno.
- Función exponencial: Es única porque se deriva sin cambiar de forma: su tasa de crecimiento es proporcional a su valor.
Aprende cuáles son las reglas básicas de una derivación ¡aquí!
Diferencias entre derivada, diferencial y tasa de cambio
Derivada
- Representa el límite de la razón de cambio entre dos variables.
- Es la herramienta matemática que mide la pendiente de la recta tangente a una curva en un punto.
Ejemplo: la derivada de la posición respecto al tiempo es la velocidad.
Diferencial
- Es un pequeño incremento o variación infinitesimal en una variable.
- Se denota como 𝑑𝑥 o 𝑑𝑦, y se usa en aproximaciones o en el cálculo integral.
Ejemplo: si 𝑦=f(𝑥), entonces 𝑑𝑦= f'(𝑥)𝑑𝑥
Tasa de cambio
- Es la interpretación práctica de la derivada en contextos reales.
- Describe cómo una magnitud varía respecto a otra en un intervalo de tiempo o espacio.
Ejemplo: el crecimiento de una población por año, o la aceleración de un coche.
Tipos de derivadas
Derivada de una constante
La derivada de una constante siempre es cero, ya que su valor no cambia sin importar la variable. Por ejemplo, si 𝑓(𝑥) =7, entonces 𝑓'(𝑥) =0. Esto refleja que la pendiente de la recta horizontal es nula.
Derivada de una función lineal, polinómica, exponencial, logarítmica y trigonométrica
Cada tipo de función tiene reglas particulares dentro del proceso de derivación:
Estas derivadas fundamentales permiten calcular de manera directa sin recurrir siempre a la definición formal con límites.
Derivadas de orden superior
Cuando aplicamos la operación de derivación más de una vez, obtenemos derivadas de orden superior:
- Segunda derivada: mide la concavidad de una curva y, en física, representa la aceleración.
- Tercera derivada y superiores: se usan en estudios avanzados de movimiento, oscilaciones y optimización.
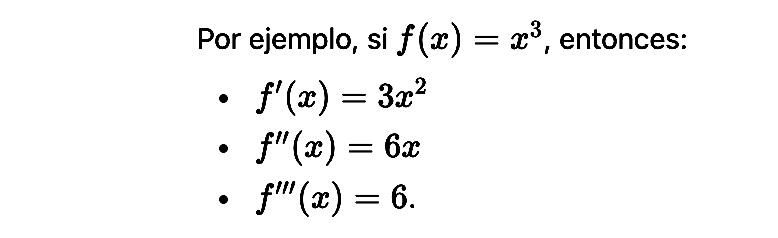
Estas derivadas sucesivas ayudan a comprender no solo cómo cambia una función, sino cómo cambia la manera en que cambia.
Propiedades de la derivada
Linealidad
La propiedad de linealidad nos dice que si una función está formada por una suma o resta de varias expresiones, podemos derivar cada parte por separado y luego juntar los resultados. Esto hace que el proceso sea mucho más sencillo y ordenado.
Regla del producto y del cociente
Cuando una función resulta de multiplicar o dividir dos expresiones distintas, no basta con derivarlas de forma aislada: se deben combinar siguiendo reglas específicas. La regla del producto asegura que el cambio de una función afecte también al cambio de la otra, mientras que la del cociente se encarga de manejar correctamente las divisiones, evitando errores comunes al trabajar con numeradores y denominadores.
Regla de la cadena
Esta es quizá ¡una de las reglas más importantes! Se aplica cuando tenemos una función compuesta, es decir, una función dentro de otra. La regla de la cadena nos permite desarmar esa composición paso a paso, para entender cómo cada parte contribuye al cambio total. Es esencial en problemas de física, economía e ingeniería, porque muchas veces los fenómenos reales no se describen con funciones simples, sino con combinaciones más complejas.
¿Para qué sirven las derivadas? Aplicaciones prácticas
Aplicaciones en física: velocidad, aceleración y movimiento 🚀
La derivada expresa la velocidad instantánea como el límite cuando el tiempo tiende a cero, y la aceleración como la derivada de la velocidad.
En economía: maximización de beneficios y minimización de costos 💰
Se usan para encontrar máximos y mínimos de funciones de producción, ingresos o costos.
En ingeniería y otras disciplinas científicas ⚙️
La derivación permite modelar materiales, sistemas eléctricos o fenómenos dinámicos.
Optimización en problemas del mundo real 🌍
El más claro ejemplo de que las matemáticas ¡pueden vivir más allá de las páginas! Encontrar la mejor solución en transporte, recursos o logística depende de aplicar las derivadas.
Derivadas en el aprendizaje avanzado
Relación con las integrales
Las derivadas no están solas en el cálculo: siempre caminan de la mano con las integrales. Mientras que la derivada mide el cambio instantáneo de una función, la integral se encarga de medir la acumulación de esos cambios a lo largo de un intervalo. Esta dualidad es tan importante que recibe el nombre de Teorema Fundamental del Cálculo, y es la base del análisis matemático moderno.
Papel de las derivadas en ecuaciones diferenciales
Muchas leyes de la naturaleza, como la difusión del calor, el crecimiento de una población o la dinámica de un resorte, se expresan mediante ecuaciones diferenciales. Estas ecuaciones incluyen derivadas que describen cómo evoluciona un sistema en el tiempo o en el espacio. Resolverlas permite predecir comportamientos y modelar fenómenos complejos en física, biología, economía e ingeniería.
Introducción a derivadas parciales y derivadas implícitas
Cuando trabajamos con funciones de varias variables, aparecen las derivadas parciales (partial derivatives), que permiten analizar el cambio de una función respecto a una sola variable, manteniendo las demás fijas. Por otro lado, la derivada implícita surge en funciones que no están expresadas de forma directa (por ejemplo, relaciones entre 𝑥 e 𝑦 dentro de una misma ecuación). Ambas son herramientas fundamentales en matemáticas superiores, ya que permiten abordar problemas más realistas y multidimensionales.
Síntesis del artículo
¿Ahora lo ves? La derivada es una herramienta universal: describe cambios, mide pendientes y permite interpretar el comportamiento de funciones en el mundo real ¡siendo las bases del cálculo moderno!
Y es que, como lo has podido ver, estas definen cómo cambia una función en un punto, poseen reglas y propiedades de la derivada específicas y permiten resolver problemas de física, economía o ingeniería.
Así que, ten la certeza de con práctica en ejercicios de derivación y el apoyo de los nuestros expertos en Superprof Chile, cada estudiante puede dominar los tipos de derivadas, aplicar el teorema fundamental y entender profundamente qué es la derivada en el contexto del análisis matemático.
¿Te gustó este artículo? ¡Evalúalo!
Loading...
