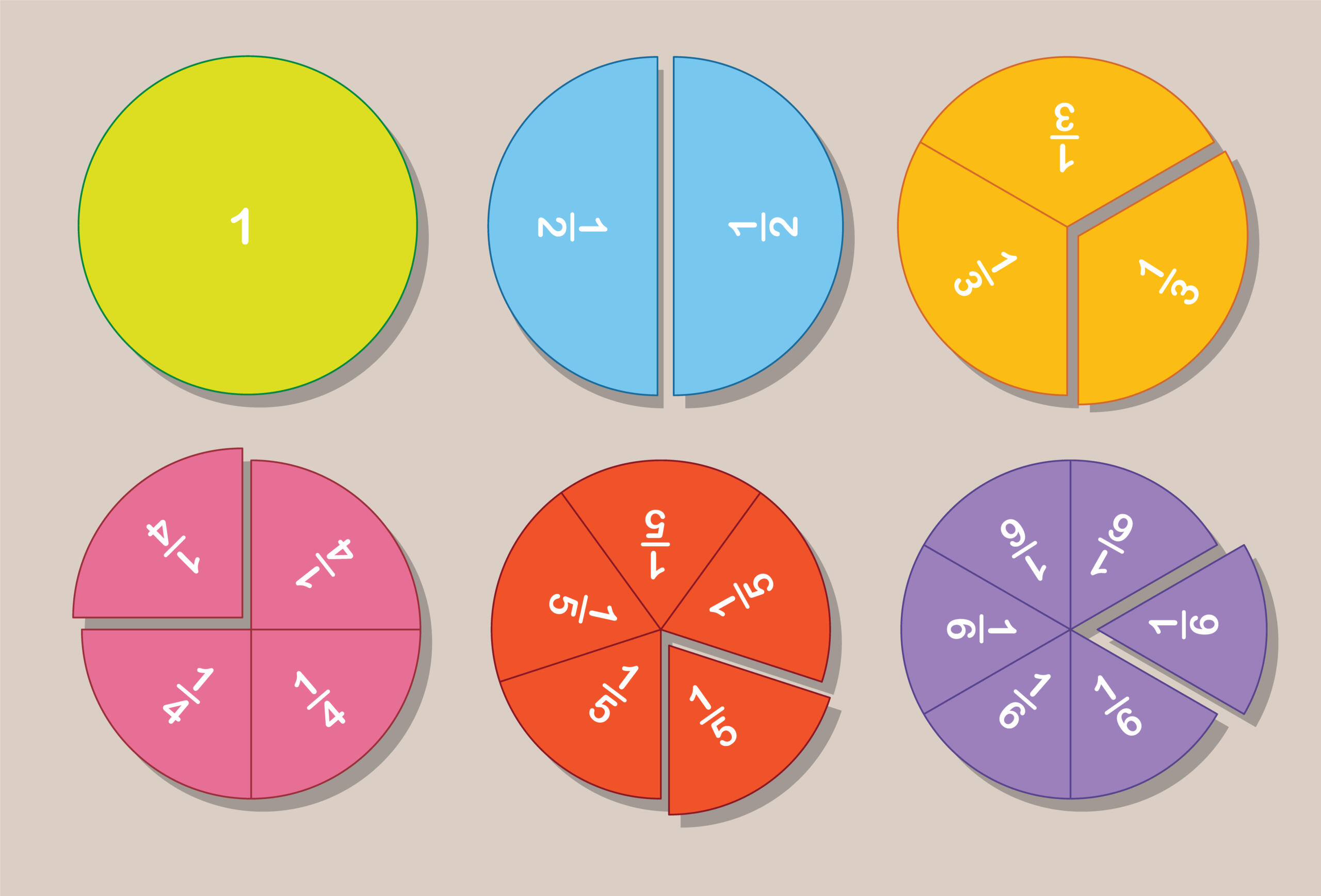
Sabemos que pueden existir múltiples confusiones a la hora de sumar y restar fracciones. Pero no te preocupes, estamos aquí para poder ayudarte.
Este artículo contiene diferentes ejemplos y ejercicios, explicados paso a paso y en forma sencilla, para que puedas entender todo lo que respecta a adición y sustracción de números racionales (Q).
Sigue leyendo y descubre la mejor forma para realizar operaciones con fracciones, solucionar los problemas más comunes y entender el mundo de los números racionales en su totalidad.

Adición de números racionales: ¿Cuál es su ejecución?
Los números racionales se pueden sumar y restar, pero, por supuesto, estas operaciones obedecen a ciertas reglas de ejecución.
Definición de adición de números racionales
Lo primero que debemos entender es cuáles son los componentes de las fracciones que vamos a sumar. Por ejemplo, en una fracción que es 2/8, ¿Cómo se llama el número de arriba y cómo se llama el número de abajo?
2/8
- El número 2 es el numerador.
- El número 8 es el denominador.
Para poder sumar dos fracciones el denominador de ambas debe ser el mismo. Por ejemplo, ¿Cómo sumaríamos 2/8 + 4/8?
Ambas fracciones tienen el mismo denominador, que es el número 8. Como el denominador es el mismo, se tiene que sumar solo el 2 más el 4, y mantener el denominador. Esto se grafica de la siguiente forma:
2/8 + 4/8= 6/8
Al resultado lo podemos simplificar, teniendo en cuenta que 6 y 8 son múltiplos de 2. Entonces, esta suma de números racionales simplificada quedaría en 3/4.
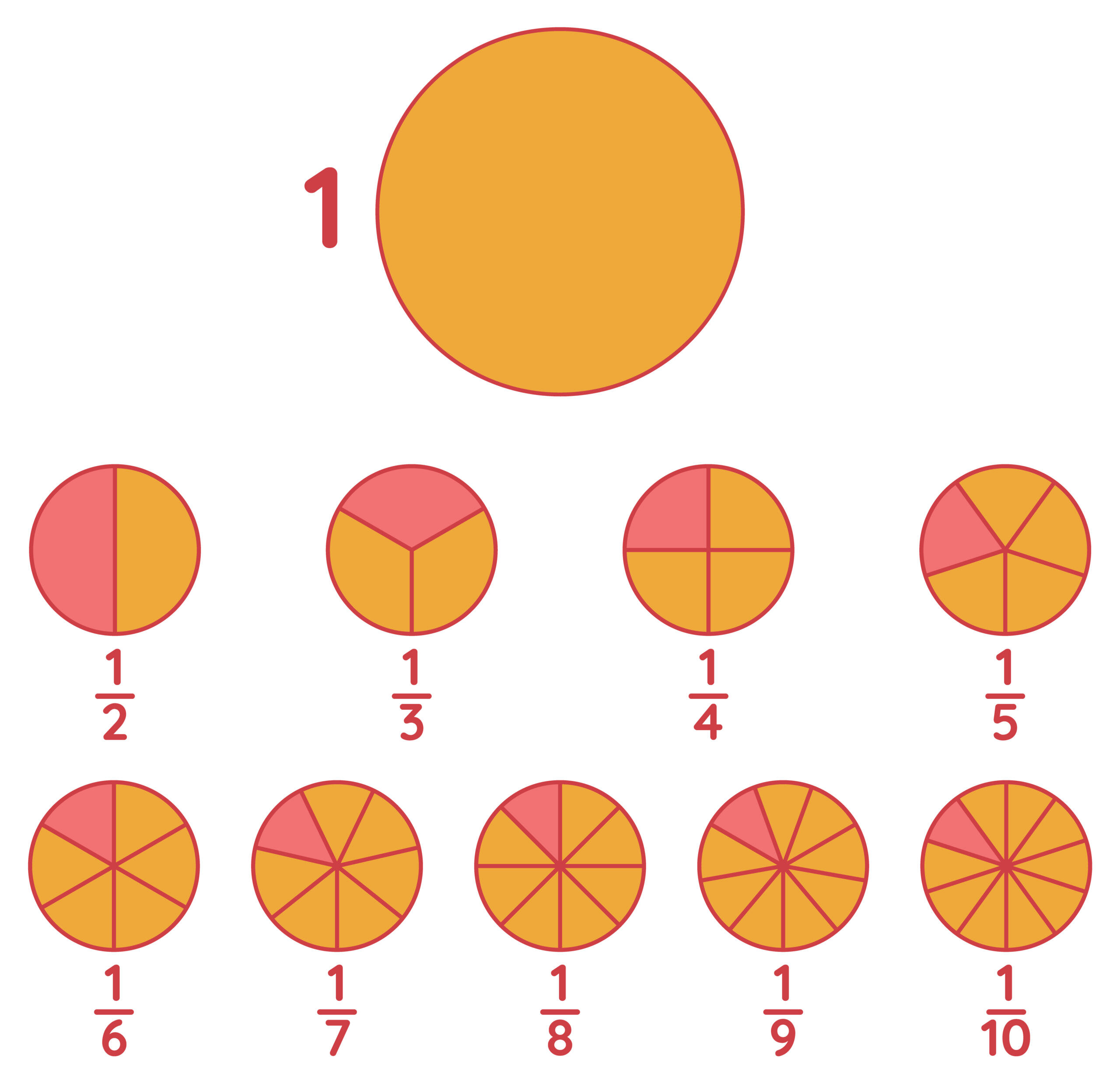
Pero también se puede sumar fracciones con distintos denominadores. Para esto hay que buscar el mínimo común denominador (mcd) entre ambas fracciones.
Esto quiere decir que cuando dos fracciones tienen diferentes denominadores, hay que igualar los denominadores para que ambas se puedan sumar.
Por ejemplo, si tenemos dos fracciones con diferente denominador: 1/4 y 2/3. Para sumarlas tenemos que encontrar el mínimo común denominador, que es el número más pequeño que es múltiplo de estos dos números, o sea, del 4 y del 3. En este caso sería el 12
Para dejar la primera fracción con denominador 12 tenemos que multiplicarla por 3, mientras que la segunda la tenemos que multiplicar 4. Entonces quedaría:
3/12 + 8/12= 11/12
Esta suma también se puede hacer multiplicando ambos denominadores y luego multiplicando de manera cruzada extremos con extremos de las fracciones, para luego sumar los resultados.
1/4 y 2/3 = (1x3) + (4x2)/12= 11/12
Ahora, si las fracciones tienen signo positivo o negativo tienes que considerar siempre la regla de los signos. Los números racionales no escapan a estos.
- (-) + (-) = (-)
- (+) + (+) = (+)
Si los símbolos son opuestos, hay que realizar la operación y restar, y el signo que queda corresponde al número mayor.
Sustracción de números racionales
La adición y sustracción de números racionales tienen las mismas reglas operativas. Esto quiere decir que, para restar dos fracciones, al igual que en la suma, ambas deben tener el mismo denominador.
Revisemos a continuación, ejemplos de suma y resta de números racionales:
3/5 – 2/5 = 1/5
Pero ¿Qué pasa si 2/5 tiene símbolo negativo? La operación quedaría de la siguiente forma:
3/5 – (-2/5) =
Lo que hay que hacer ahora es seguir la regla de los signos. Revisemos la siguiente tabla:
| Combinación | Resultado |
| (+) - (+) | Resta normal. |
| (+) - (–) | Pasa a ser suma. |
| (–) - (+) | Queda negativo. |
| (–) - (–) | Queda en suma negativa. |
Por lo tanto, esta cifra quedaría de la siguiente manera:
3/5 – (-2/5) =
Si hay dos negativos, se transforma en positivo:
3/5 + 2/5= 5/5= 1
Descubre a continuación todo sobre la multiplicación y división de números racionales.
Sustracción de números racionales y más ejemplos de adición
Ejemplos básicos con fracciones y decimales
Lo primero que tienes que saber es cuál es la forma que tienen los números racionales. Pongamos como ejemplo al número 5.
El número 5 se puede expresar también de la siguiente forma 5/1. Porque 5 dividido en 1 es igual a 5. Todos los números enteros se pueden escribir como fracción.
Pero también en los racionales podemos encontrar números que no son enteros. Por ejemplo, 1/2 o 3/4. Pero ¿por qué estos números son racionales? Porque la división que se produce es un número exacto.
- 1/2 = 0.5
- 3/4 = 0,75

Pero ¡ojo!, los decimales de los resultados tienen que ser exactos o periódicos (que se extiendan hacia el infinito con un mismo número).
Es por esto que la suma y sustracción de números racionales deben tener mismo denominador. En el caso contrario, arrojaría un resultado que no sería un número racional.
Ejemplos avanzados con diferentes denominadores
¿Sabías que existen fracciones mixtas? Las fracciones mixtas mezclan un número entero con una fracción. Estas fracciones se escriben de la siguiente forma:
3 1/2
Para poder hacer operaciones se tiene que transformar la fracción mixta en impropia. Una fracción impropia es aquella en que el numerador es igual o mayor al denominador. Para hacer la conversión hay que realizar la siguiente operación.
2 3/4
Hay que multiplicar el número entero, en este caso el 2, por el denominador, el 4, y sumarle el numerador, o sea el 3. En este caso quedaría así:
2x4+3 / 4 = 11/4
Ahora para transformar una fracción impropia a mixta se debe realizar la siguiente operación. Trabajemos con la fracción 7/3:
7/3
Lo primero que tenemos que hacer es dividir el numerador 7 por el denominador 3. El resultado será 2, con un resto de 1. La fracción mixta quedaría entonces de la siguiente forma: 21/3
Encuentra en este artículo más operaciones combinadas con números racionales.
Pensemos ahora en lo siguiente, ¿Qué pasa si tenemos un número con decimales periódicos? Por ejemplo, el número 0,3 periódico, donde el 3 se extiende hacia el infinito.
Para poder hacer esta transformación debemos primero aplicar álgebra. Digamos que 0,3 es igual a X.
X=0,3
Ahora a esta ecuación la vamos a multiplicar por 10 y va a quedar:
10x= 3,3
Lo siguiente es restar la ecuación original o sea X=0,3. Entonces quedaría:
10x-x= 3,3-03
9x=3
X=3/9
X=1/3
De esta forma transformamos (y comprobamos también) que 0,333333 (periódico) es igual a 1/3.
Prueba de adición de números racionales en la vida cotidiana
¿Para qué voy a estudiar esto si nunca lo voy a aplicar en la vida real? No es eso lo que muchos estudiantes se preguntan alguna vez en la vida. Bueno, esta duda no aplica para las matemáticas, ni menos para los números racionales.

La suma y resta de números racionales, y su correcto manejo, te puede ayudar a desenvolverte de mejor forma en situaciones como:
- Calcular impuestos.
- Chequear descuentos.
- Aplicación de una receta.
Incluso para repartir una pizza los números racionales te serán útiles.
¿Dónde usamos la adición y sustracción de números racionales en la vida diaria?
Usamos los números racionales cuando analizamos nuestras finanzas, por ejemplo: si deseas ahorrar todos los meses 1/3 de tu dinero, entonces estás aplicando fracciones.
Cuando cocinamos también tenemos que usar números racionales: las recetas suelen tener instrucciones relacionadas con fracciones, como por ejemplo:
- 1/2 cucharada sopera de sal.
- 3/4 de leche.
Si hacemos alguna manualidad de carpintería también usamos números racionales: si quieres dividir una tabla de 1 metro en tres, y luego usas 2/3 de la madera, eso es un cálculo de fracciones. Además, profesores matemáticas recomiendan revisar los cálculos para evitar errores.
Como ves, los ejemplos de adición y sustracción de números racionales son muchos, y todos están presente en nuestras actividades diarias. Si buscas siempre vas a encontrar aplicaciones de los números racionales en la vida real.
Práctica diaria de fracciones
Siempre es bueno que practiques la adición y sustracción de números racionales para que estés listo ante cualquier cálculo que necesites hacer. Recuerda que las fracciones están presentes en nuestra vida en diferentes circunstancias.
Para practicar puedes usar el clásico método de ejercicios en papel. o puedes aprovechar todas las ventajas que te entrega la tecnología actual y acceder a aplicaciones como Khan Academy. Además, un profesor matemática puede ofrecerte nuevas estrategias.
Recuerda también que la práctica mental siempre es un buen ejercicio, tanto para manejar mejor la matemática como para tener un cerebro más activo y sano. Además, profesores matemáticas recomiendan seguir entrenando la mente.
Síntesis del artículo
En este artículo aprendimos en profundidad cómo se realiza la suma y resta de números racionales. También vimos diferentes ejercicios que involucraban uso de fracciones y números con decimales.
Entendimos también qué eran las fracciones mixtas e impropias, y tomamos consciencia de la gran importancia de los números racionales en nuestra vida cotidiana.
Resumir con IA: